Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Categoria de Tecnologia
Postado em 23 abril 2023
Atualizado em 23 abril 2023
Palavras-chave: point,virgula,comma,fixed,fixo,fp,flutuante,fracao,valor,math,matematica,calculo,aritmetica
Visualizações: 1536
O ponto flutuante começou a ser utilizado em computadores residenciais com o intuito de dar mais flexibilidade e precisão para aplicativos que exigiam cada vez mais desempenho da máquina. A partir de então, a unidade responsável por todas as tarefas envolvendo ponto flutuante passou a ser integrada ao processador de cada vez mais computadores, possibilitando a execução de softwares que exigem cálculos com números fracionados com precisão. Hoje em dia é difícil encontrar um computador que não tenha um FPU (Unidade de ponto flutuante) embutida no seu processador.
Porém, o ponto flutuante pode ser custoso para alguns dispositivos que não exigem tanta complexidade. Por isso, alguns dispositivos optam por não utilizar o FPU. Essa decisão pode trazer benefícios como:
Sistemas embarcados, alguns jogos de videogame e dispositivos de áudio (DSP - Digital signal processor) dispensam o ponto flutuante. Mesmo assim, esses dispositivos ainda podem expressar números contendo uma porção fracionária usando o ponto fixo.
O ponto fixo pode ser considerado o antônimo do ponto flutuante. Em inglês, é chamado de “fixed point”. Como o próprio nome diz, o ponto fixo não pode ser deslocado após a sua localização ser definida. Em outras palavras, o ponto fixo que separa a parte inteira e a parte fracionário de um valor, não pode ser deslocado posteriormente. Isso acontece pelo fato da parte inteira e fracionária serem calculados de forma separada.
O número acima possui duas partes:
Toda máquina opera usando o sistema de numeração binário. Por isso, o número acima deve ser convertido para a numeração binária. Porém, antes de converter para a numeração binária é necessário especificar onde o ponto fixo vai ser colocado. Para especificar a localização do ponto fixo usa-se a notação Q.
A notação Q ou formato Q é usado para expressar o formato de um valor com ponto fixo. Por exemplo, se tivéssemos 4bits, poderíamos armazenar 4 dígitos binários (), isso permitiria que armazenássemos um valor decimal de 0 até 15. Porém, se tivermos um valor fracionário precisaríamos de alguns dos 4bits para representar a parte fracionária do valor. No caso do 7,5 precisaríamos de 3 bits para representar o número 7 e 1 bit para representar o número fracionário:
Nesse caso, expressamos o formato do ponto fixo com UQ3.1, pois são 3 dígitos para o 7 e 1 dígito para o 0,5. O “U” na frente do “Q” representa a palavra “unsigned”, cujo significado é “sem sinal”, portanto esse formato não suporta sinal negativo e não pode representar valores negativos.
Por exemplo, o formato Q5.10 teria um tamanho de 16 bits (w = 16): 1 bit para o sinal, 5 bits para a parte inteira e 10 bits para a parte fracionária. Se usarmos o formato UQ4.12, teríamos um tamanho de 16 bits (w = 16): 4 bits para a parte inteira e 12 bits para a parte fracionária.
O símbolo “w” é usado para representar o tamanho (quantidade de bits). O w pode ser calculado da seguinte forma:
O número (1) pode ser removido caso o formato seja unsigned (sem sinal).
Imagine que temos um valor com o formato UQ4.4 com um w de 8 bits e queremos transformar o número em numeração binária. Primeiro, transformamos a parte inteira (m) em binário:
Em seguida, transformamos a parte fracionária (n) em binário:
É possível perceber que a parte inteira e a parte fracionária devem ser calculados de modo diferente, enquanto a parte inteira divide, a parte fracionária multiplica.
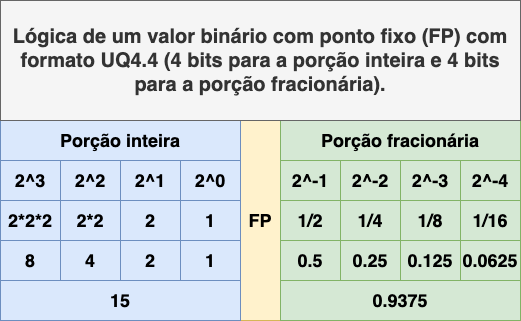
Visualizando a imagem acima, usando o ponto fixo com formato UQ4.4 podemos perder precisão para expressar alguns valores. O cálculo vai dar o valor mais aproximado dentro dos limites do formato proporcionado. Para saber a faixa que a notação Q pode cobrir usamos o esquema abaixo:
| Notação | Faixa de valores representáveis |
|---|---|
| Signed Qm.n | |
| Unsigned UQm.n |
Por exemplo, o formato Q8.8 pode representar um valor dentro de uma faixa com valor mínimo de -128.0 até o valor máximo de 127.99609375 que pode ser representado com . Caso o formato fosse UQ8.8 essa representação poderia mudar para 0 que é uma faixa com valor mínimo de 0 até o valor máximo de 255.99609375.
Contas de adição, subtração, multiplicação e divisão também são possíveis usando o ponto fixo.
Por exemplo, imagine números representados em 8 bits com o formato de UQ4.4. Se tivermos os números e , o resultado deverá ser . Se transformados para números binários, os números são respectivamente:
O resultado da soma acima será de que é .
Mais uma vez usando números de 8 bits com o formato de UQ4.4, temos os seguintes valores:
O resultado da subtração acima será de que é .
A multiplicação de dois números com ponto pode ser realizado do modo convencional, porém exige um passo extra que é o deslocamento do ponto para a esquerda (shift). Veja o exemplo abaixo:
Ao multiplicar o número acima por ele mesmo teremos . No processo de multiplicação em binários, a seguinte resolução será efetuada:
Repare que após a multiplicação um shift de duas casas do ponto para a direita é realizado para que o resultado final correto seja obtido.
Assim como a multiplicação, a divisão com dois valores contendo ponto fixo também pode ser feita do modo convencional. Para facilitar, podemos usar a mesma técnica que aplicamos na resolução decimal, deslocando a vírgula duas casas para a direita:
A divisão usando os mesmos valores em forma binária devem trazer o mesmo resultado que acima.
O ponto fixo foi substituído pelo ponto flutuante em muitos casos, mas ainda continua sendo adotado e utilizado em ocasiões onde a precisão e a flexibilidade dos cálculos não é tão importante. Mesmo assim, o ponto fixo tem um custo bem menor, tendo um desempenho melhor em questão de velocidade. Porém, o melhor desempenho depende do contexto geral, incluindo muitos outros elementos decisivos.
Além da imprecisão de resultados, os cálculos envolvendo ponto fixo exigem que os números estejam ajustados na mesma escala, isso é, os dois valores devem ter pontos fixos em locais iguais, tendo formatos iguais.
Projetos práticos

Convertendo imagens para ascii art usando o valor da intensidade das cores cinzentas.
Programando um jogo clássico de arcade usando javascript e p5.js. O usuário deve quebrar os blocos utilizando uma bola ao mesmo tempo que evita que a bola saia pela parte inferior da tela
Projeto de criação de um sistema de busca usando o framework Symfony e Elasticsearch. A integração com Kibana também é feito de modo remoto com um raspberrypi.
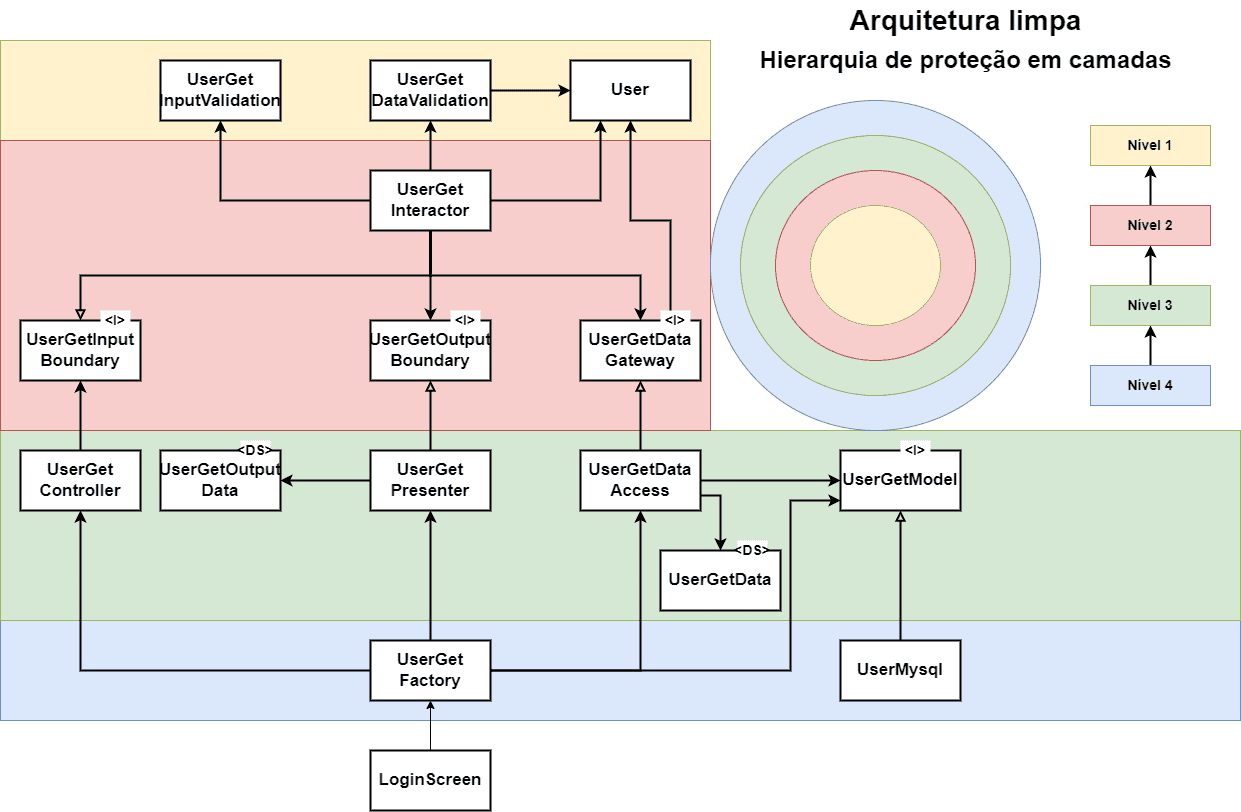
Usando JavaFX e arquitetura limpa para criar um aplicativo de caixa eletrônico extremamente simples.
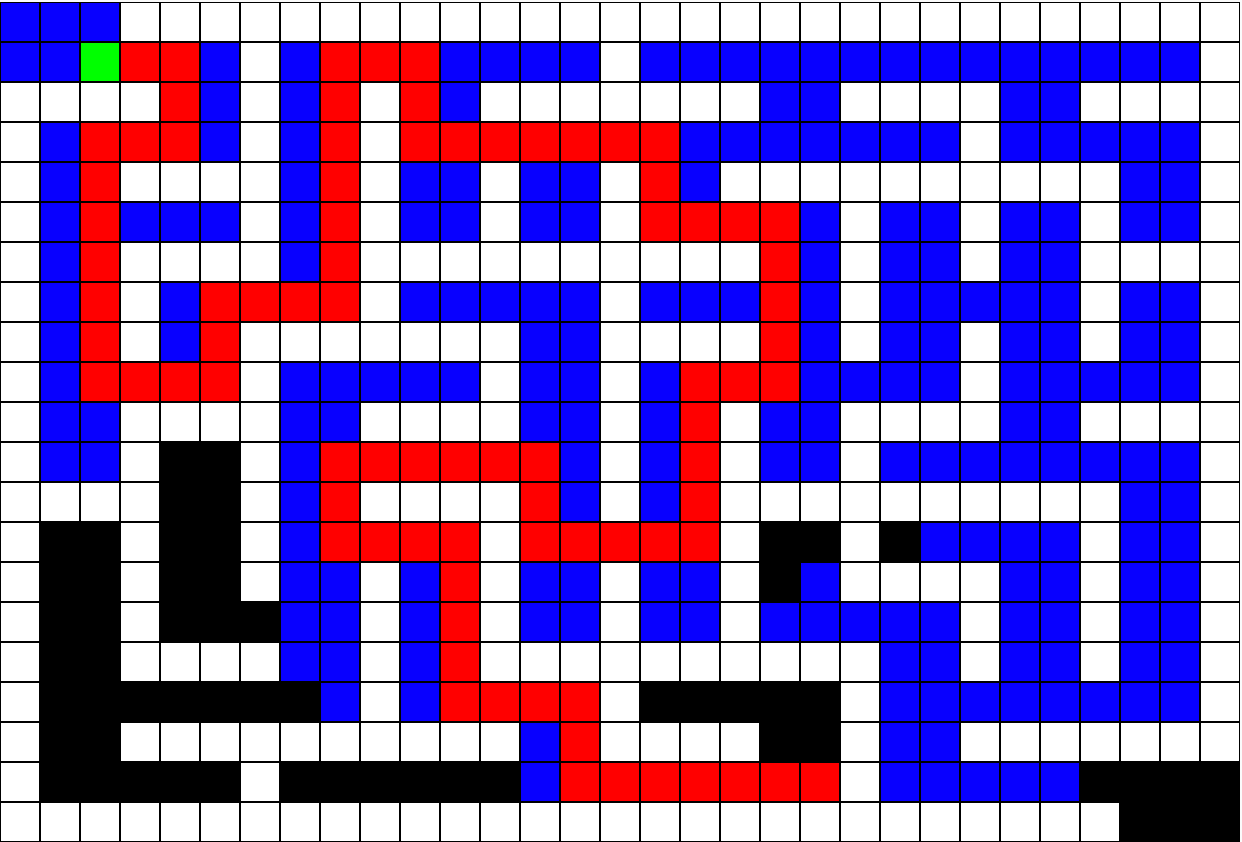
Implementando um programa que encontra a menor distância entre dois pontos dentro de um labirinto usando o algoritmo A* (a-estrela).

Os algoritmos na ciência da computação são o principal meio para o desenvolvedor poder escrever instruções para o computador, operando a sua maneira

A política de privacidade é obrigatória para qualquer site que utiliza dados pessoais do usuário. Porém, quais dados são esses especificamente?
Interface dedicada ao desenvolvedor ou especialista da computação para executar comandos ao computador sem a presença de um mouse.
Data Science ou ciência de dados, é uma área de computação que se concentra em extrair informações valiosas de grandes quantidades de dados.
O PERT é um método composto por linhas e nós conectados entre si com o intuito de representar a dependência entre as atividades.
Caracterizam uma grandeza física que possui módulo, direção e sentido. Pode simular eventos como queda, atração e deslocamento de objetos em um meio.