Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Categoria de Management
Postado em 15 novembro 2022
Atualizado em 15 novembro 2022
Palavras-chave: pert,tecnica,avaliacao,revisao,programa,atividade,gerenciamento,calculo,formula
Visualizações: 2342
O gerenciamento de um projeto pode ser um grande problema quando não sabe-se ao certo quanto tempo cada atividade pode necessitar.
Felizmente, existem diversos métodos de management disponibilizados na internet para o auxilio do gerenciamento, o PERT é um desses métodos.
PERT é a sigla para “Program Evaluation and Review Technique”, em português pode ser traduzido para técnica de avaliação e revisão de programa.
Esse método é composto por linhas e nós conectados entre si com o intuito de representar a dependência entre as atividades. A dependência entre atividades acontece quando uma atividade só pode ser iniciada após a finalização de outra atividade. Além disso, as atividades podem ser executadas de modo paralelo.
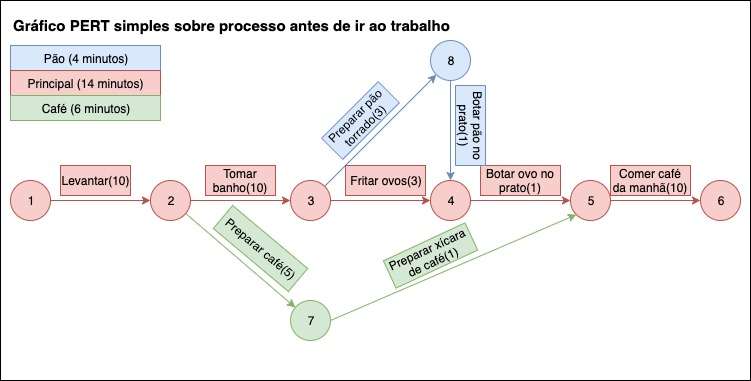
Um grande número de atividades pode trazer grandes problemas e imprevistos para um gestor. Além do tempo médio que uma atividade pode necessitar, outros fatores também devem ser levados em consideração, como tempo otimizado e tempo pessimista.
O início e o fim de cada atividade impacta no tempo total de um projeto, pois muitas atividades só podem ser iniciadas após a conclusão de outras tarefas.
Usando o método PERT é possível encontrar fatores decisivos desde a tomada de decisões até o orçamento de um projeto. Entre alguns desses fatores estão:
Usando o método PERT obtêm-se um gráfico que facilita a interpretação das atividades e evita o desperdício de tempo devido a imprevistos que podem vir a acontecer durante o projeto.
O caminho crítico é o caminho com tempo de maior duração, consequentemente sendo o valor que representa o tempo mínimo necessário para finalizar o processo inteiro.
Antes de desenhar o gráfico PERT, cria-se uma tabela com as atividades e suas dependências. A tabela pode ser montada como mostra no exemplo a seguir:
| Atividade | Dependência |
|---|---|
| A | - |
| B | - |
| C | A |
| D | B |
| E | C, D |
A tabela acima mostra que as atividades A e B não possuem dependências, pois podem ser iniciadas a qualquer momento sem nenhuma condição. A atividade C só pode ser iniciada após a atividade A ser concluída, assim como a atividade D só pode ser iniciada após a atividade B está finalizada. A última atividade E, depende das atividades C e D para poder ser iniciada.
Uma vez que temos as dependências, podemos criar o gráfico PERT:
O tempo de estimativa é calculado a partir de três elementos:
Mais uma vez, criamos uma tabela contendo os três elementos acima:
| Atividade | Dependência | to | tm | tp |
|---|---|---|---|---|
| A | - | 2 | 4 | 12 |
| B | - | 3 | 4 | 5 |
| C | A | 1 | 2 | 3 |
| D | B | 2 | 3 | 4 |
| E | C, D | 1 | 4 | 7 |
A unidade do elemento tempo é arbitrária, podendo ser segundos, minutos, horas, dias, meses, anos, etc…
O método PERT possui uma fórmula para calcular a estimativa de tempo de duração de cada atividade.
O símbolo te representa o tempo estimado. Ao usarmos a fórmula acima, temos os seguintes resultados:
| Atividade | to | tm | tp | te |
|---|---|---|---|---|
| A | 2 | 4 | 12 | 5 |
| B | 3 | 4 | 5 | 4 |
| C | 1 | 2 | 3 | 2 |
| D | 2 | 3 | 4 | 3 |
| E | 1 | 4 | 7 | 4 |
Também é possível calcular a variante de cada atividade usando a fórmula abaixo:
A variante é o tempo que o tempo de estimativa pode variar.
| Atividade | to | tp | variante |
|---|---|---|---|
| A | 2 | 12 | |
| B | 3 | 5 | |
| C | 1 | 3 | |
| D | 2 | 4 | |
| E | 1 | 7 | 1 |
O caminho crítico é o caminho com mais duração. O projeto só é finalizado quando o caminho crítico é concluído.
| Atividade | Dependência | te |
|---|---|---|
| A | - | 5 |
| B | - | 4 |
| C | A | 2 |
| D | B | 3 |
| E | C, D | 4 |
Lembrando que o “te” é a estimativa de duração de cada atividade, montamos o gráfico e calculamos o caminho crítico.
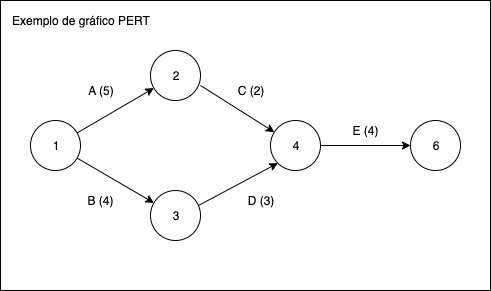
O gráfico acima possui dois caminhos, 1-2-4-6 e 1-3-4-6. Nesse caso, os dois caminhos possuem o mesmo tempo de duração. Portanto a duração será de 11 dias.
Suponhamos que devemos terminar o projeto em um prazo de 13 dias. Já calculamos o tempo de duração do caminho crítico, tempo médio de cada atividade e a variante. Com esses três elementos podemos calcular a probabilidade de concluir o projeto dentro do prazo de 13 dias.
Apesar dos dois caminhos terem o mesmo tempo de duração, a variante dos caminhos é diferente, como podemos ver a seguir:
O gráfico PERT do projeto tem dois caminhos. Calculamos as variantes de cada atividade presente no caminho.
Nesse caso, o caminho com maior variante será selecionado, pois tem maior escala de variação.
A fórmula para calcular a probabilidade de terminar o projeto dentro prazo é a seguinte:
O x representa o prazo de 13 dias, o M é a soma do tempo médio das atividades do caminho crítico que é 11 (5+2+4) e a variante é a soma das variantes do caminho crítico que é .
Logo teremos a seguinte equação:
O resultado obtido foi 0,52. Para obtermos o resultado final precisamos analisar a tabela de distribuição normal padrão.
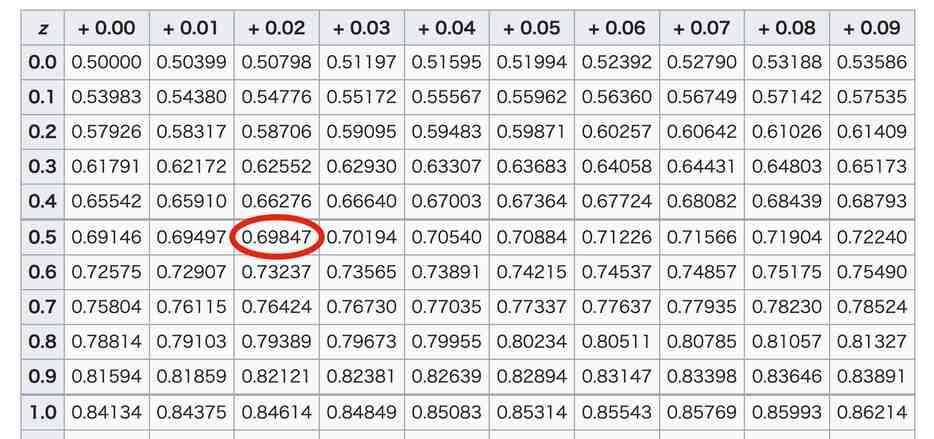
Assim, conclui-se que a probabilidade de terminar o projeto dentro do prazo de 13 dias é de 69%.
O PERT é um método que auxilia no gerenciamento de projetos contendo fórmulas já definidas para utilização.
Projetos práticos
Programando um jogo clássico de arcade usando javascript e p5.js. O usuário deve quebrar os blocos utilizando uma bola ao mesmo tempo que evita que a bola saia pela parte inferior da tela

Desenvolvimento de um sistema de monitoramento que exibi todos os eventos que acontecem na garagem automatizada, como abertura de portões ou ocupação de vagas.

Projeto de comunicação entre dois dispositivos ESP8266 e Raspberrypi4. Laravel irá funcionar como servidor e receptor de dados de temperatura e umidade coletados com o DHT11.
Implementando um programa que encontra a menor distância entre dois pontos dentro de um labirinto usando o algoritmo A* (a-estrela).

Desenvolvimento dos conceitos mais básicos do clássico pacman, como: mapa, animação, deslocamento e detector de colisões.

Poluição do ar, solo e água ainda é um grande problema para ser resolvido ainda em vários países. Há estudos que comprovam que os países mais poluentes podem causar câncer...

Esperávamos horas para baixar apenas alguns megabytes. Nessas horas, quando o telefone tocava nós fazíamos de tudo para não atender o telefone. Mas infelizmente nem sempre dava certo....
Técnica de sistemas computacionais que dividi tarefas em estágios e executa de forma simultânea, diminuindo o tempo total de processamento.
O modelo PoC visa em avaliar uma nova tecnologia ainda não comprovada com uma demonstração, com o intuito de avaliar a sua veracidade.
Pilha e fila são tipos de estrutura de dados que contribuem para um gerenciamento de dados mais inteligente e eficaz na programação
Faz cálculos aritméticos com números fracionários usando notação científica, economizando mais bits. Também chamado de vírgula flutuante.