Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Categoria de Programação
Postado em 22 setembro 2022
Atualizado em 22 setembro 2022
Palavras-chave: busca,binaria,linear,notacao,grande,o,problema,solucao,programacao,algoritmo,tecnica,metodo
Visualizações: 3199
Métodos de aprimoração de algoritmo tem sido desenvolvidos ao longo da história da programação. Hoje, por mais que uma máquina seja poderosa, ela pode ser influenciada pelas técnicas de algoritmo.
Em algumas ocasiões onde um grande volume de dados de entrada tem que ser processados, determinadas técnicas de algoritmo devem ser implementadas.
Um bom exemplo é uma função de busca. Alguns sistemas possuem milhares de registros no banco de dados. Portanto, procurar registro por registro pode ser prejudicial para a experiência do usuário. Nesse caso, uma boa técnica a ser implementada é a busca binária.
A busca binária é uma técnica de algoritmo de busca de algum dado específico dentro de uma lista.
Essa técnica visa em dividir a lista pela metade até encontrar o elemento de busca. Eliminando elementos desnecessários, etapas desnecessárias também serão eliminadas, consequentemente melhorando o desempenho do algoritmo.
Porém, a lista precisa estar em ordem para funcionar de modo legítimo. Portanto, listas fora de ordem não irão ter suas buscas efetivamente efetuadas.
Adotando a busca binária pode-se melhorar a velocidade dos métodos de busca. Diferente de técnicas como busca linear, também conhecido por “algoritmo de força bruta”, a busca binária elimina elementos que podem ser ignorados.
Utilizando um meio de medição como a notação do grande O, a busca binária pode ser classificada como O(logn), isso quer dizer que o desempenho da busca binária pode ser classificada como excelente.
Mesmo em cenários onde volumosos dados de entrada são processados, a busca binária não apresenta grandes custos de processamento, exigindo menos da máquina e melhorando a experiência do usuário.
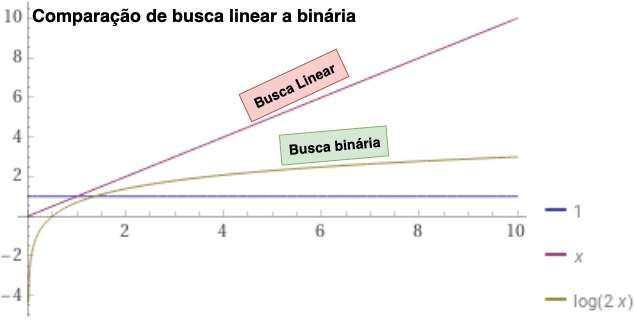
A imagem acima apresenta o nível de processamento necessário conforme os dados de entrada aumentam.
A busca binária tradicional usa 3 variáveis:
Responsável por armazenar o índice mais baixo da lista. Geralmente inicia-se com o número zero.
Armazena o valor da lista contendo o índice mais alto. Geralmente inicia-se com o número de itens dentro da lista.
Resultado da soma do mínimo e máximo, divido pelo número 2:
Lembrando que essa variável representa o índice e não o valor de cada registro da lista.
// Valor: alfabeto
// Índice: número
$list = [
0 => 'a',
1 => 'b',
2 => 'c'
];
A busca binária usa o método de divisão de conquista que visa em dividir os problemas até que eles se resolvam sozinhos.
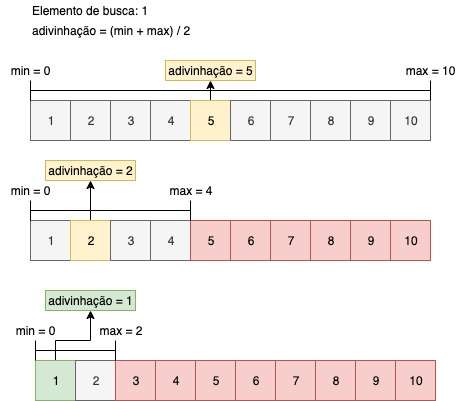
O processo repete-se enquanto a variável “máximo” continua maior do que a variável “mínimo”.
Em cada repetição, a variável “adivinhação” irá possuir o resultado.
Caso esse resultado seja maior do que o elemento de busca, esse resultado irá ser utilizado para sobrepor a variável “máximo”. Caso o resultado seja menor do que o elemento de busca, a variável “mínimo” irá ser sobreposta pelo resultado e terá o número um somado:
| Condição | Sobrepõe |
|---|---|
| Resultado == Busca | - |
| Resultado > Busca | Máximo = Resultado - 1 |
| Resultado < Busca | Mínimo = Resultado + 1 |
A representação do algoritmo de busca binária pode ser representada pelo fluxograma abaixo:
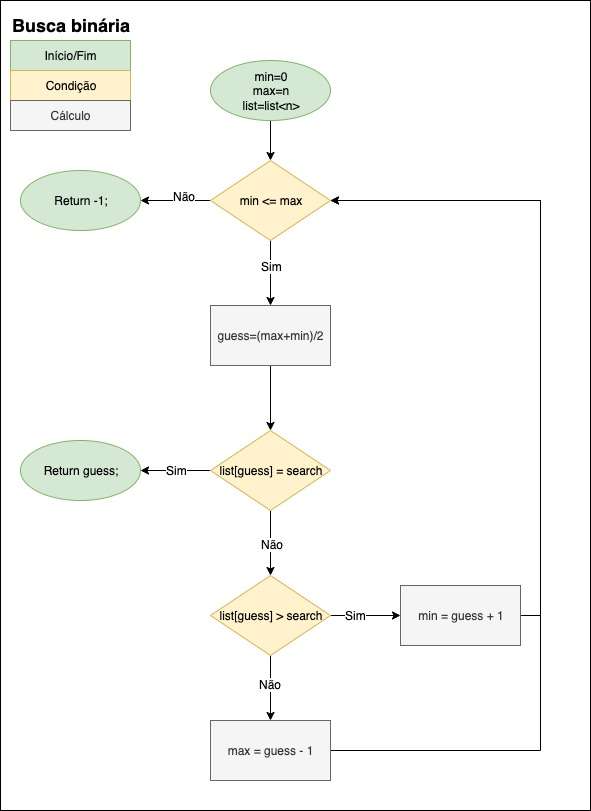
O termo “busca binária” vem do inglês “binary search”. Tem esse nome pelo fato de dividir a lista em dois pedaços em cada repetição, usando duas variáveis, “min” e “max”.
A implementação da busca binária na prática pode ser escrito com o algoritmo abaixo:
function doBinarySearch($search, $array) {
$min = 0;
$max = count($array);
while ($min <= $max) {
$guess = floor(($min + $max) / 2);
if ($array[$guess] == $search) {
return $guess;
}
if ($array[$guess] > $neddle) {
$max = $guess - 1;
} else {
$min = $guess + 1;
}
}
return null;
}
Usando uma lista, a função acima retornará os seguintes resultados:
$list = [1,2,3,6,8,10,12,15,20,21,22,25,30,37,38,39,40,42,45,48,51,55,57,61,64,67,68,70,71,72,73,74,75,76,77,78,79,80,85,90,91,92,93,94,95,96,97,99];
// retorna 0
echo doBinarySearch(1, $list);
// retorna 47
echo doBinarySearch(99, $list);
// retorna 23
echo doBinarySearch(61, $list);
// retorna nulo
echo doBinarySearch(9, $list);
A busca pode ser uma boa alternativa para substituir algoritmos de força bruta, graças a sua simplicidade e efetividade. Esse método utiliza técnica de divisão e conquista, onde o problema é dividido em pequenos problemas até que se resolva sozinho.
Para funcionar de modo correto, a busca binária necessita que os items da lista estejam em ordem.
Projetos práticos
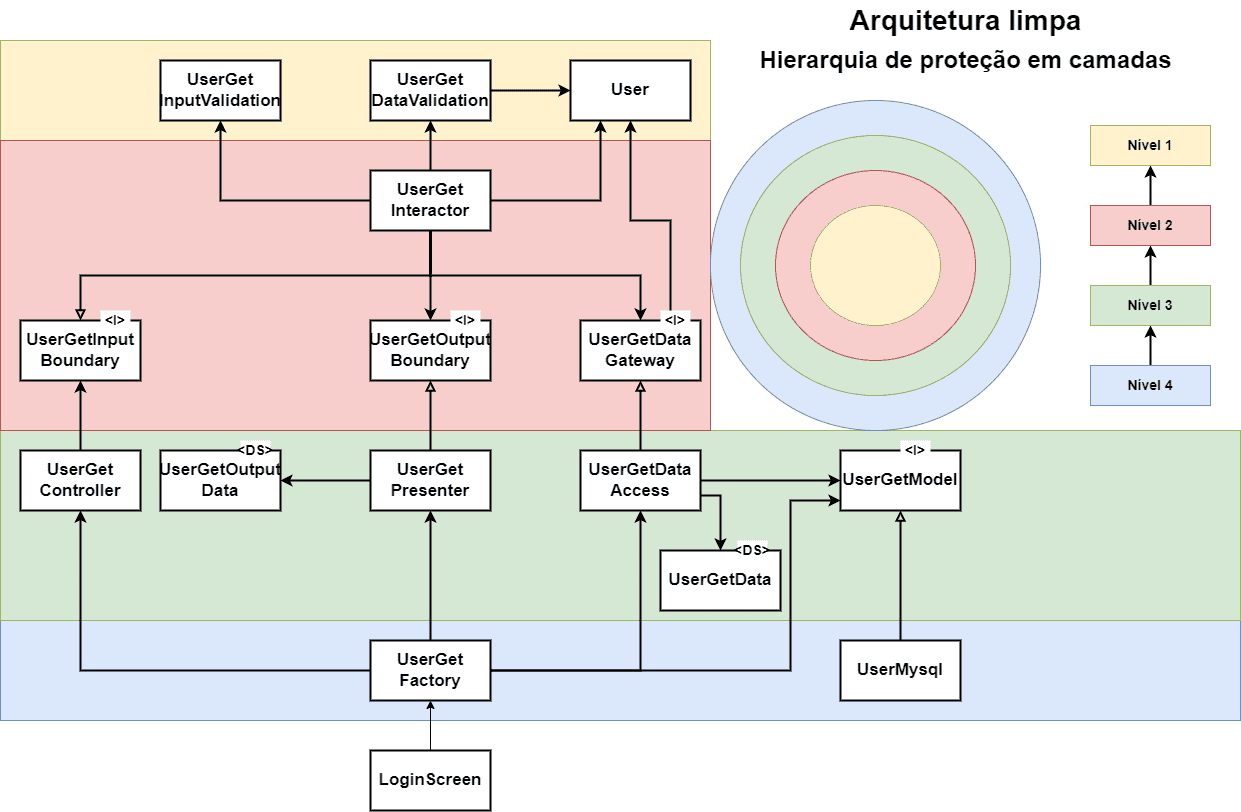
Usando JavaFX e arquitetura limpa para criar um aplicativo de caixa eletrônico extremamente simples.
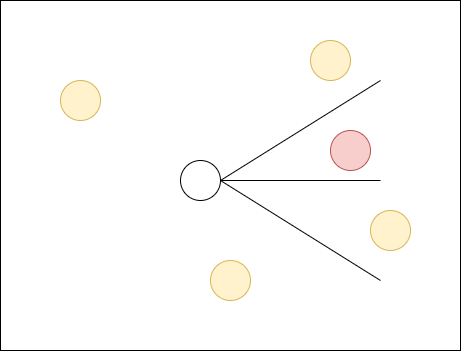
Detectando objetos que entram dentro do campo de visão do personagem. Útil para servir de "gatilho" para eventos em um jogo.
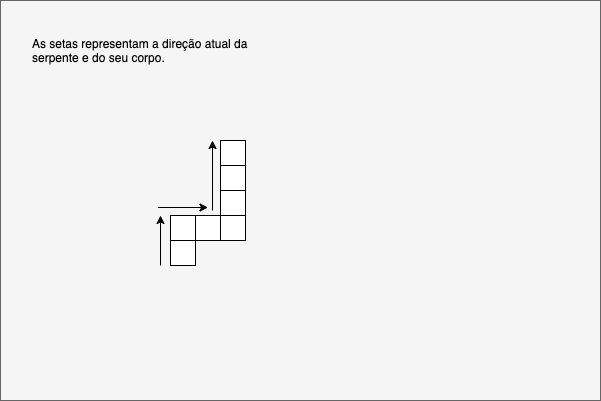
Programando o clássico jogo da serpente usando o framework p5.js. Tutorial indicado para iniciantes da programação que querem aprender os conceitos básico da área criando jogos.
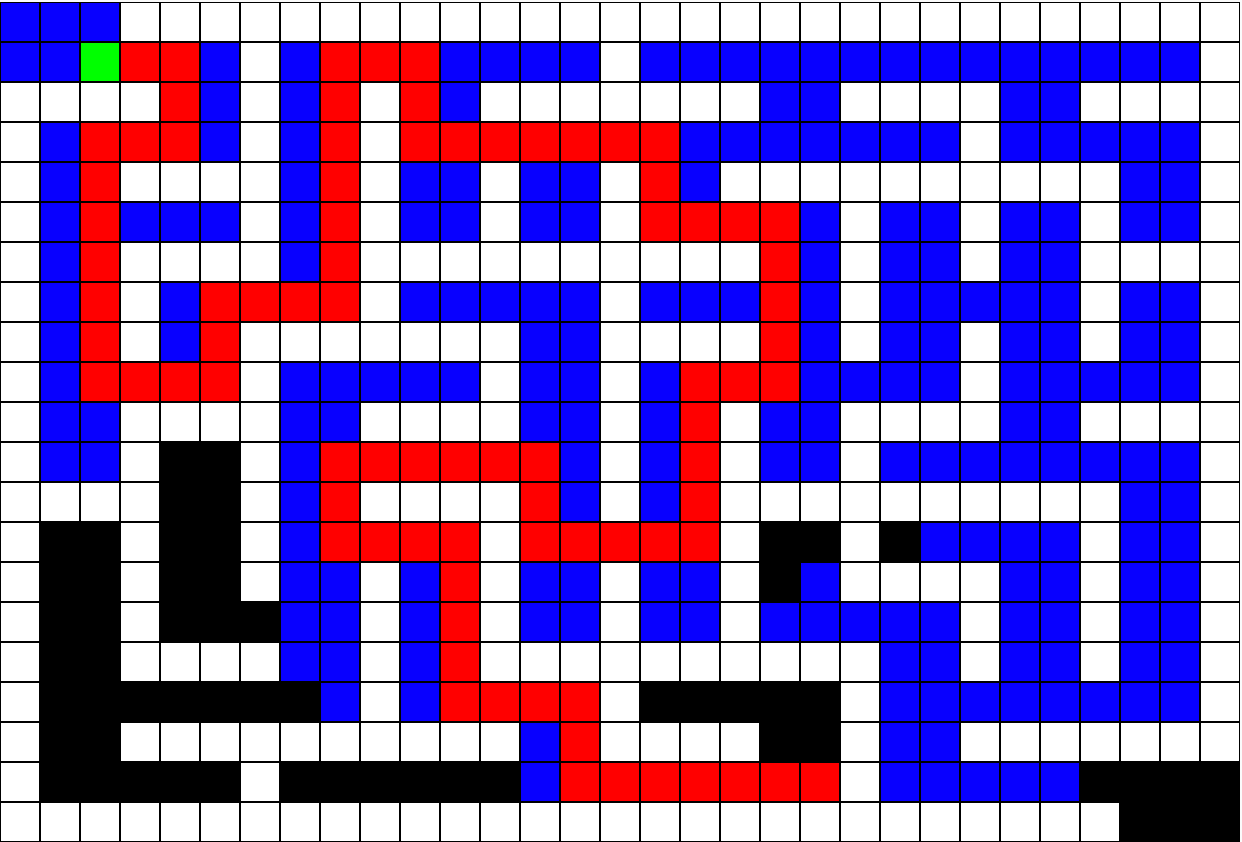
Implementando um programa que encontra a menor distância entre dois pontos dentro de um labirinto usando o algoritmo A* (a-estrela).

Desenvolvimento dos conceitos mais básicos do clássico pacman, como: mapa, animação, deslocamento e detector de colisões.

Antes de podermos visualizar o site, o endereço que digitamos na barra de endereço do nosso navegador passa por várias etapas, para só então podermos visualizar o site pela primeira vez...

Uma rede interna sem um firewall é como se fosse uma casa com a porta destrancada. Um indivíduo com más intenções pode se aproveitar para a invadir quando menos esperamos.
A notação do O grande é um método de fácil implementação, usado para avaliar a eficiência de um algoritmo em relação ao tempo de processamento.
Caminhos entre os componentes do computador que são responsáveis pela transferência de informações de controle, endereçamento e dados.
Design thinking é um método bastante flexível que procura atender os desejos humanos com o intuito de inovar ou solucionar problemas.
Fornece conexão com a rede para dispositivos móveis mesmo quando estes se encontram em deslocamento. Utiliza o protocolo LTE para a transferência de dados.