Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Categoria de Programação
Postado em 20 agosto 2022
Atualizado em 20 agosto 2022
Palavras-chave: grande,ozão,big,notation,notação,programacao,eficiencia,algoritmo
Visualizações: 4757
Os algoritmos são a base para o funcionamento de qualquer dispositivo digital. Hoje, a programação possui diversos tipos de linguagens, com suas respectivas vantagens.
É notável o avanço da tecnologia, principalmente na área de computação. Computadores com alta capacidade de armazenamento e processamento abriram portas para novas tecnologias como BigData e Deep Learning.
Entretanto, por mais que as máquinas tenham se tornado mais poderosas, a importância do bom funcionamento do algoritmo sempre foi requerido.
Um algoritmo bem programado pode consumir bem menos memória, evitando uso excessivo do CPU e oferecendo uma experiência melhor ao usuário.
Mas na programação, o cenário mais importante é o pior cenário, pois a disponibilidade é um fator indispensável na segurança da informação.
Um método bastante utilizado ao redor do mundo para medir a disponibilidade de um serviço é a notação big-O.
Esse método também é chamado de notação O grande.
Notação big-O é um método utilizado para medir a eficiência de um algoritmo de forma simples e prática.
Esse método usa os dados de entrada como base para calcular o tempo de processamento de um algoritmo. Quanto mais dados de entrada a serem processados, mais uma máquina tende a demorar até chegar ao resultado final.
A notação big-O é usada para medir o tempo de processamento de um algoritmo, porém o pior cenário possível é o cenário que mais importa aos programadores.
Caso uma máquina chegar ao seu limite de processamento devido a um algoritmo mal implementado, isso pode trazer sérias consequências ao funcionamento, prejudicando principalmente a disponibilidade do serviço.
Obviamente, conforme o número de dados de entrada aumenta, o tempo de processamento da máquina também aumenta. A notação big-O ajuda a analisar se uma máquina mediana suporta ou não o algoritmo no pior cenário possível.
É certo que dependendo da eficiência da máquina, o resultado pode ser diferente. Porém, o principal foco desse método é a eficiência do algoritmo independente da eficiência da máquina.
A notação do O grande é uma notação assintótica, que utiliza termos para classificar o algoritmo.
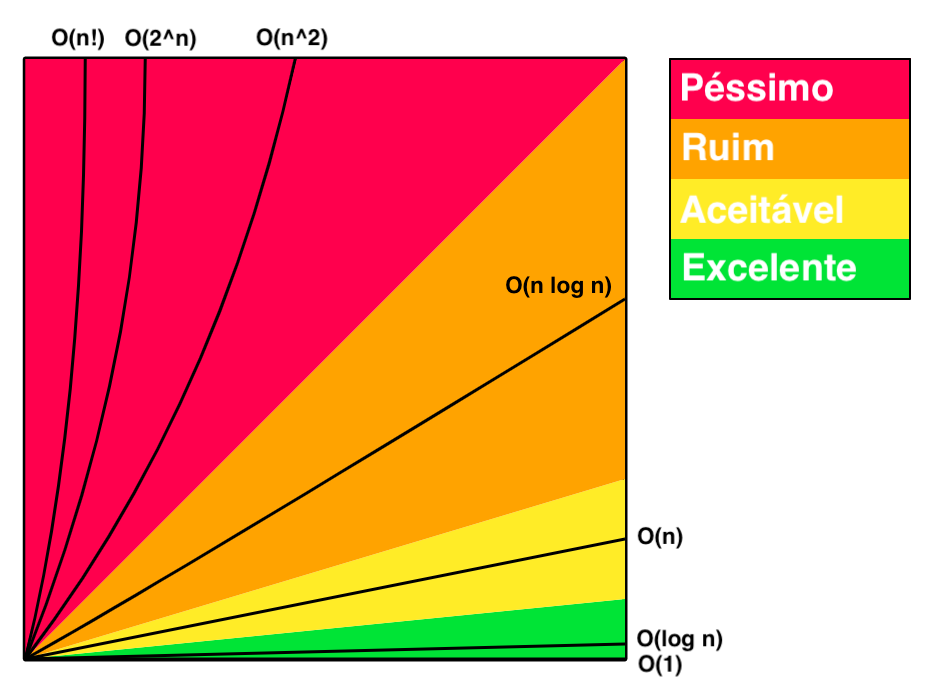
Observa-se no gráfico acima, a diferença no tempo de processamento (eixo Y) conforme a quantidade de dados de entrada aumenta (eixo X).
Esse método possui duas regras básicas:
A porção do algoritmo com maior custo de tempo de processamento torna-se o resultado final.
A ordem dos termos são:
O(1) < O(log n) < O( Sqrt(n) ) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n)
Se um algoritmo possui uma porção O(1) e outra O(n), temos a conta abaixo:
Porém, nesse exemplo o termo dominante é o termo com a pior performance, portanto teremos como resultado final apenas:
Outros exemplos:
Algoritmos contendo múltiplas porções com mesmo custo de processamento, não se repetem.
O exemplo abaixo não é correto:
A constante deve ser omitida, reproduzindo o resultado abaixo:
Considere o seguinte algoritmo:
function calcular() {
return 15 * (30 + 90);
}
print(calcular());
O exemplo de algoritmo acima apenas realiza um pequeno cálculo. No caso acima, não há repetições, portanto o tempo de demora é representado como O(1).
Ao utilizarmos loops dentro do algoritmo o resultado pode variar um pouco:
function calcular(int $no) {
return 15 * ($no + 90);
}
foreach ($i = 0; $i < 1000; i++) {
print(calcular($i));
}
No exemplo acima, temos um loop com 1000 repetições. Nesse caso podemos fazer a seguinte afirmação:
Porém, na notação do O grande, não se escreve dessa maneira uma vez que precisamos analisar os dados de entrada. Por isso, devemos escrever da seguinte forma:
Quando temos um loop dentro do outro, temos repetições de repetições:
function calcular(int $no1, int $no2) {
return 15 * ($no1 + $no2);
}
foreach ($i = 0; $i < 1000; i++) {
foreach ($j = 0; $j < 1000; j++) {
print(calcular($i, $j));
}
}
No algoritmo acima, o número de processos é elevado ao quadrado:
Assim como no algoritmo abaixo, o número de processos é elevado a 3:
function calcular(int $no1, int $no2, int $no3) {
return $no3 * ($no1 + $no2);
}
foreach ($i = 0; $i < 1000; i++) {
foreach ($j = 0; $j < 1000; j++) {
foreach ($k = 0; $k < 1000; k++) {
print(calcular($i, $j, $k));
}
}
}
Resultado:
Em alguns casos, não há como evitar o alto custo de processamento. Porém, geralmente é possível otimizar esses processos utilizando técnicas de programação adequadas. Alguns exemplos disso são:
Um bom exemplo de otimização de algoritmos é a utilização de estruturas de dados de modo apropriado, como por exemplo a pilha e a fila.
Se compararmos com o arranjo (array), temos a seguinte tabela:
+--------------------+---------------------------------------------------------------------------+
| Estrutura de dados | Complexidade temporal |
| +-------------------------------------+-------------------------------------+
| | Cenário intermediário | Pior cenário |
| +--------+-------+----------+---------+--------+-------+----------+---------+
| | Acesso | Busca | Inserção | Remoção | Acesso | Busca | Inserção | Remoção |
+--------------------+--------+-------+----------+---------+--------+-------+----------+---------+
| Arranjo (Array) | O(1) | O(n) | O(n) | O(n) | O(1) | O(n) | O(n) | O(n) |
+--------------------+--------+-------+----------+---------+--------+-------+----------+---------+
| Stack (Pilha) | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) |
+--------------------+--------+-------+----------+---------+--------+-------+----------+---------+
| Queue (Fila) | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) |
+--------------------+--------+-------+----------+---------+--------+-------+----------+---------+
Observando a tabela acima, podemos chegar a conclusão que a utilização de arranjos (array) para acessar dados em uma estrutura de dados é potencialmente mais efetivo do que a pilha e a fila, mesmo no pior dos casos.
Porém, na inserção e remoção de dados de uma estrutura, a pilha e a fila são muito mais eficientes do que o arranjo.
Ao utilizar os pontos fortes de estruturas em cenários apropriados, pode-se obter melhores resultados.
A busca linear é um algoritmo sequencial, também considerado um algoritmo de força bruta. Algoritmos que utilizam a força bruta, terão sua performance prejudicada caso um grande número de dados de entrada seja utilizado.
A busca linear é um algoritmo que dividi os dados de entrada até encontrar o valor procurado. Dividir os dados pela metade até encontrar o elemento alvo é uma excelente abordagem para melhorar o tempo de processamento.
A notação do O grande é um método de fácil implementação, usado para avaliar a eficiência de um algoritmo em relação ao tempo de processamento.
Esse método é de extrema utilidade quando analisamos o pior cenário possível, no qual uma enorme quantidade de dados seriam passados como entrada.
Ao analisar o pior cenário, é possível chegar a conclusão da necessidade ou não da otimização de um algoritmo.
Projetos práticos
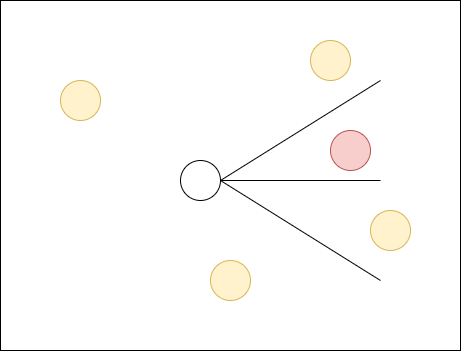
Detectando objetos que entram dentro do campo de visão do personagem. Útil para servir de "gatilho" para eventos em um jogo.
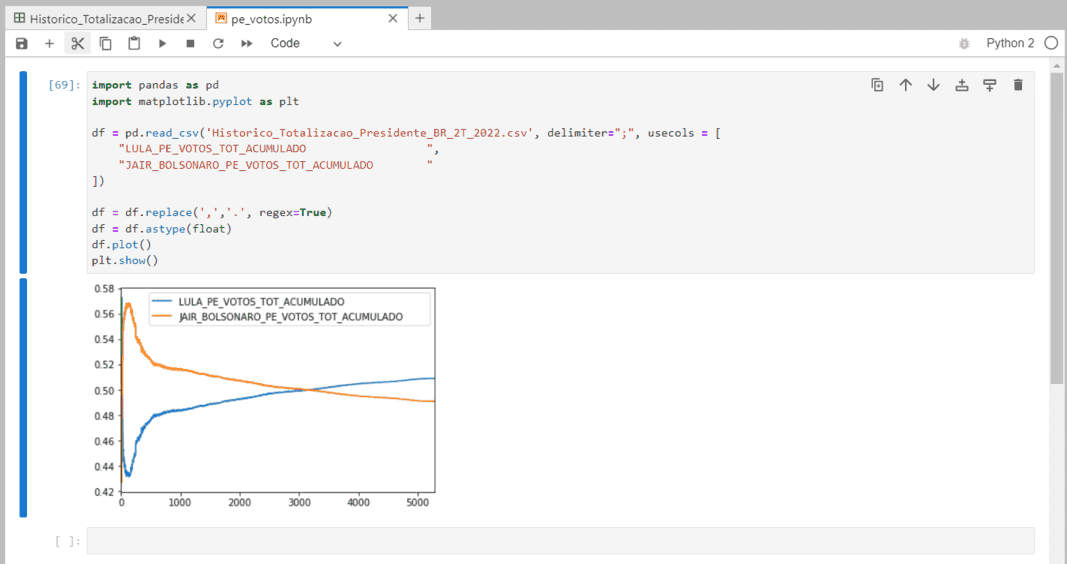
Simulação dos gráficos do segundo turno das eleições presidenciais, utilizando python e ferramentas de análise de dados, pandas e jupyter.
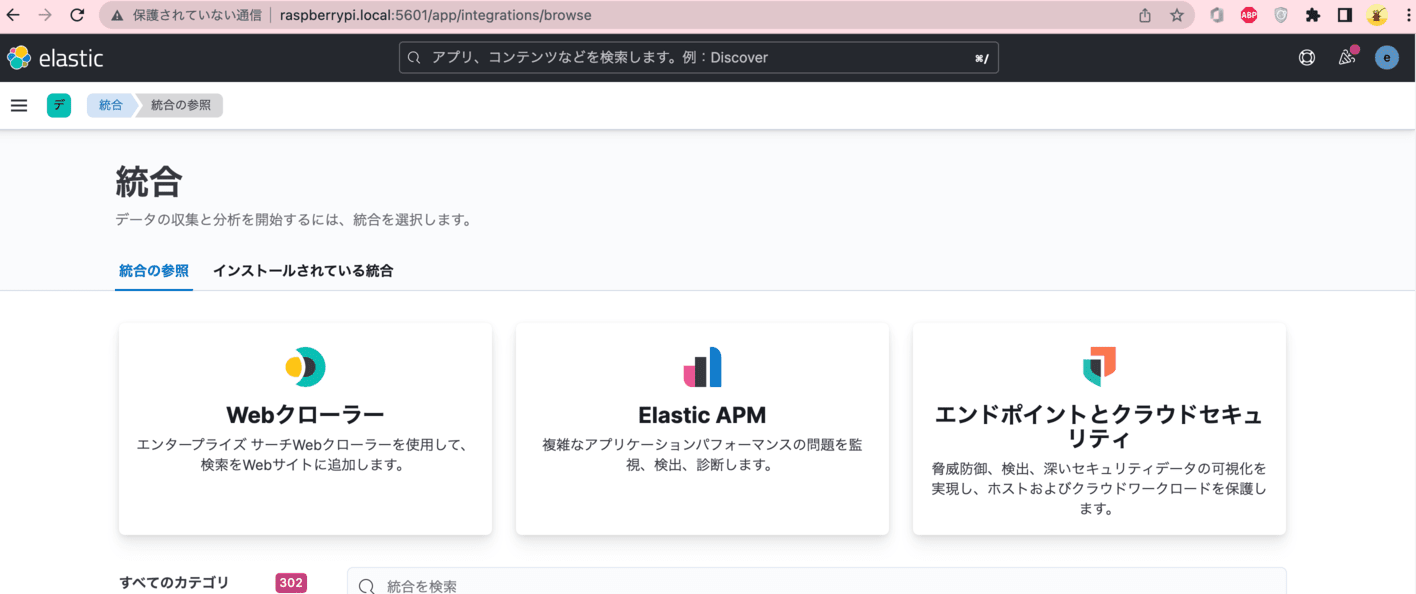
Projeto de criação de um sistema de busca usando o framework Symfony e Elasticsearch. A integração com Kibana também é feito de modo remoto com um raspberrypi.
Programando o clássico jogo da serpente usando o framework p5.js. Tutorial indicado para iniciantes da programação que querem aprender os conceitos básico da área criando jogos.
Programando um jogo clássico de arcade usando javascript e p5.js. O usuário deve quebrar os blocos utilizando uma bola ao mesmo tempo que evita que a bola saia pela parte inferior da tela

Alguns desses protocolos é o HTTP que usamos em nossos navegadores. Sem esses protocolos teríamos alguns problemas na comunicação de dispositivos através da internet.

Antigamente o endereçamento de dispositivos era feito manualmente, porém isso traz muitas dificuldades em questão de administração. O DHCP resolve esses problemas
Caracterizam uma grandeza física que possui módulo, direção e sentido. Pode simular eventos como queda, atração e deslocamento de objetos em um meio.
Subcampo da inteligência artificial inspirado no sistema de neurônios de seres inteligentes como o dos humanos, permitindo com que as máquinas aprendam.
Técnica de algoritmo que faz o agente vagar pelo ambiente virtual sem um destino definido. Esse comportamento pertence ao steering behaviors.
Conjunto de técnicas de algoritmo que simulam comportamentos realísticos. Usado em jogos e em pesquisas biológicas para o estudo de comportamentos.