Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Categoria de Programação
Postado em 25 março 2023
Atualizado em 25 março 2023
Palavras-chave: matematica,vetor,fisica,programacao,variavel,modulo,direcao,sentido,x,y
Visualizações: 1326
No desenvolvimento de programas, diversos métodos de física e matemática são adotados para trazer mais coerência e efetividade ao algoritmo. No campo de desenvolvimento de jogos e na robótica, valores como gravidade, direção, ângulo e até resistência do ar são calculados para fazer simulações de eventos que acontecem na vida real.
O grande problema começa a aparecer quando determinados valores passam a possuir fortes relações entre si. Por exemplo, valores como a gravidade e a coordenada horizontal de um personagem em um plano bidimensional podem ter forte relação quando o personagem pula. Após o salto do personagem, a gravidade tende a puxar ele de volta para a superfície, alterando diretamente o valor da coordenada horizontal do personagem.
O gerenciamento dessas variáveis pode ser um grande problema quando realizado de forma separada. Os vetores são uma ótima opção para fazer o gerenciamento desses valores.
O vetor geométrico, também chamado apenas de “vetor” é uma estrutura de dados que representam um ponto ou objeto em um espaço bidimensional (2D) ou tridimensional (3D). Na física, esse vetor é usado para caracterizar uma grandeza física e é composto por três propriedades:
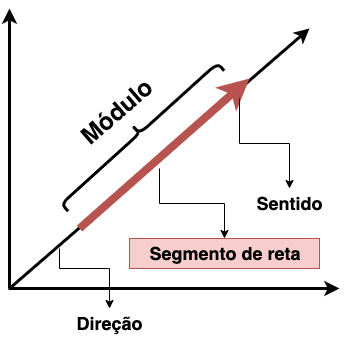
Em termos simples, o vetor pode ser considerado uma simples seta com direção, tamanho e sentido.
Na programação, o vetor geométrico pode possuir de 2 a 3 elementos para representar as coordenadas de um objeto na tela. Geralmente, esses valores são definidos como (x, y, z) no plano de três dimensões () e (x, y) no plano de duas dimensões ().
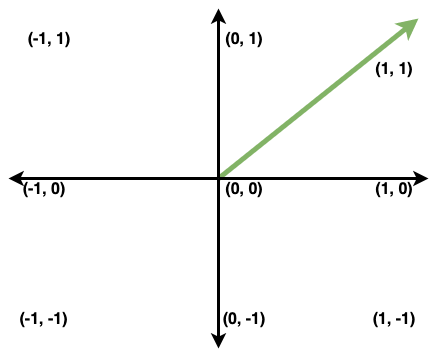
Na imagem acima, os valores mínimo e máximo são respectivamente -1 e 1. O número zero representa o centro do plano. Visualizando a seta verde podemos fazer as seguintes afirmações:
Veja abaixo um exemplo de implementação de vetores em Java:
public class Vetor {
public float x; // Armazena valor horizontal
public float y; // Armazena valor vertical
public Vetor(float x, float y) {
this.x = x;
this.y = y;
}
}
Como escrito nos comentários, a propriedade “x” armazena o valor horizontal e o “y” armazena o valor vertical do vetor. Essas são as propriedades necessárias para obter o módulo, direção e sentido do vetor.
Em fórmulas o vetor é representado por uma letra com uma seta encima.
O vetor jamais poderá ser representado apenas com um número, pois ele é um conjunto de propriedades. Entretanto, o módulo pode ser representado por um número, uma vez que isso indica a sua magnitude.
O vetor possui diversos cálculos para a obtenção de valores que são usados frequentemente no desenvolvimentos de jogos e na robótica. Alguns exemplos são:
A magnitude é o módulo do vetor. Como mostrado acima no exemplo de implementação de vetores em Java, temos apenas duas propriedades: x e y. O módulo do vetor pode ser calculado a partir desses dois valores.
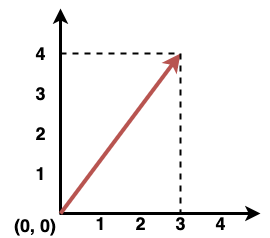
A imagem acima tem um valor de 4 na vertical e 3 na horizontal, ambos valores são respectivamente y e x. O vetor acima, tem um direção inclinada no sentido positivo diagonal formando um triângulo retângulo em relação ao plano. Não sabemos o ângulo da direção, mas temos as coordenadas x e y, que são 3 e 4. O módulo é calculado usando o teorema de pitágoras.
Se substituirmos as letras acima com os recursos que temos, obtemos a seguinte resolução:
O módulo do vetor da imagem acima é 5 e pode ser facilmente adicionado em um algoritmo. Usando o exemplo de implementação em Java, dentro da classe “Vetor”, adicionamos a função abaixo:
public float magnitude() {
return Math.sqrt(this.x * this.x + this.y * this.y);
}
Em seguida, podemos instanciar o vetor e obter a magnitude:
Vetor vetor = new Vetor(3, 4);
float modulo = vetor.magnitude(); // Resultado é 5
O módulo é um valor indispensável no cálculo de vetores e pode ser utilizado em diversas ocasiões, alguns exemplos são:
A normalização de vetores é a divisão de cada propriedade pela magnitude do vetor para transforma-lo em um valor unitário.
Normalizando o vetor podemos ter o valor proporcional de cada propriedade entre 0 e 1. Essa prática é bastante comum em situações onde queremos saber apenas a direção do vetor, recalcular a magnitude ou simplesmente para facilitar os cálculos.
Na classe “vetor”, adicionamos a função abaixo:
public Vetor normalizar() {
float magnitude = this.magnitude();
return new Vetor(this.x / magnitude, this.y / magnitude);
}
Em seguida instanciamos o vetor e normalizamos:
Vetor vetor = new Vetor(3f, 4f);
Vetor vetorNormalizado = vetor.normalizar();
System.out.println(String.valueOf(vetorNormalizado.x)); // 0.6
System.out.println(String.valueOf(vetorNormalizado.y)); // 0.8
As coordenadas x e y do vetor acima foram transformados em valores unitários de 0,6 e 0,8 respectivamente. É bastante normal multiplicar os valores unitários por números arbitrários para obter o comprimento de vetor desejado.
A aritmética de vetores é usada para soma, subtração, multiplicação e divisão de vetores. Ao calcular as coordenadas (x,y) de (3,3) e (1,2), simplesmente calculamos os valores horizontais com valores horizontais e valores verticais com valores verticais.
A regra é a mesma para cálculos de subtração, multiplicação e divisão.
O método da linha poligonal traça uma seta da origem do primeiro vetor até a extremidade do último vetor. Esse método é usado para a soma de vetores que é comutativa, portanto não importa a ordem dos vetores em uma soma.
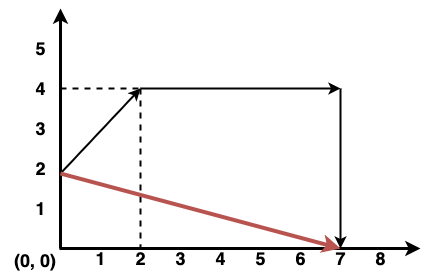
O gráfico acima possui 3 vetores. Seguindo a ordem das setas, os 2 últimos vetores tem origem na extremidade de seus antecessores. O vetor vermelho indica a soma dos 3 vetores tendo sua origem no mesmo ponto do primeiro vetor e sua extremidade no mesmo ponto do terceiro vetor. A soma dos vetores na programação pode ser realizada do modo convencional:
Usando os valores de deslocamento na vertical e horizontal com base no gráfico acima, podemos encontrar a soma do módulo dos vetores:
Pelo fato dos vetores estarem ligados entre si formando uma sequência, podemos usar o método da linha poligonal que forma um triângulo retângulo, aplicando o teorema de pitágoras.
Os resultados são quase idênticos e ambos podem ser adotados na programação no contexto necessário.
Para usar o método do paralelogramo devemos ter 2 vetores inclinados formando um ângulo. Os vetores devem estar sob o mesmo ponto de aplicação, ou seja, na mesma origem, como mostra a imagem abaixo:
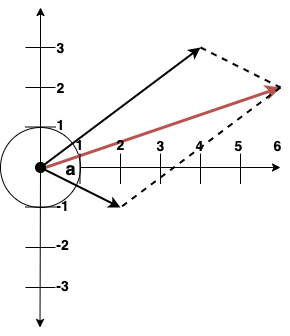
A letra “a” representa o ângulo formado pelos 2 vetores. Para descobrir o tamanho do vetor vermelho usando o paralelogramo, os vetores não podem ter as seguintes condições:
Vetores com ângulo de 0, 90 e 180 graus não podem ser calculados com o paralelogramo. Assim, podemos calcular o tamanho do vetor resultante usando a fórmula abaixo:
O gráfico acima, não possui um ângulo definido. Mas podemos descobrir o ângulo usando a fórmula abaixo:
CA é o cateto adjacente ao ângulo que estamos procurando e h é a hipotenusa. Calculando a magnitude dos cateto oposto e do cateto adjacente, teremos os valores de 5 e . Em seguida, calculamos a hipotenusa usando o teorema de pitágoras que é . Finalmente podemos descobrir o cosseno de dividindo o cateto adjacente pela hipotenusa, que dará (em torno de 0,40). Se convertemos esse valor para graus teremos 66. Uma vez que temos o ângulo, podemos aplicar a fórmula do paralelogramo:
Acima, descobrimos o módulo do vetor vermelho do gráfico acima. A conta acima pode ser complicada para humanos resolverem, mas pode ser calculadas facilmente por um computador.
public class SomaVetoresParalelogramo {
public static void main(String[] args) {
double ax = 2;
double ay = -1;
double amag = Math.sqrt(ax * ax + ay * ay);
double bx = 4;
double by = 3;
double bmag = Math.sqrt(bx * bx + by * by);
double degrees = 66.0;
double radians = Math.toRadians(degrees);
double result = Math.sqrt(amag * amag + bmag * bmag + 2 * amag * bmag * Math.cos(radians));
//Valor: 6.2525920887721105.
System.out.println("Valor: " + result + ".");
}
}
Como mostrado nos exemplos acima, um vetor não é composto apenas por um valor, mas por vários valores. Mesmo que dois vetores tenham módulos iguais, isso não significa que esses vetores sejam iguais. Na física, para dois vetores serem iguais, eles precisam das seguintes condições:
Na programação, basta compararmos os valores na horizontal e na vertical. Por exemplo, se tivermos (x1, y1) e (x2, y2), podemos fazer a seguinte comparação em um programa:
if (x1 == x2 && y1 == y2) {
// Vetores iguais
}
Uma vez que temos as coordenadas x, y e z podemos calcular muitos outros elementos necessários para simular eventos da vida real, como calcular ângulos, distâncias e velocidades.
Os vetores são essenciais para gerenciar conjuntos de valores que representam algum tipo de grandeza, seja no plano bidimensional ou tridimensional. Eles podem ser usados para armazenar informações como campo de visão da câmera, distância percorrida por frame e posição atual de um objeto na tela, podendo também simular eventos como queda, atração e repulsão de objetos.
Projetos práticos
Projeto de criação de um sistema de busca usando o framework Symfony e Elasticsearch. A integração com Kibana também é feito de modo remoto com um raspberrypi.
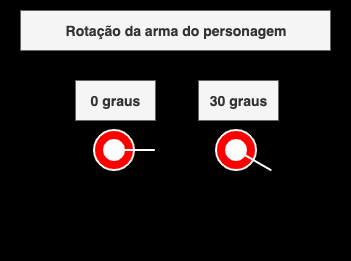
Usando lógicas matemáticas como trigonometria para criar e calcular o esqueleto de um jogo de tiro 2D em javascript

Convertendo imagens para ascii art usando o valor da intensidade das cores cinzentas.
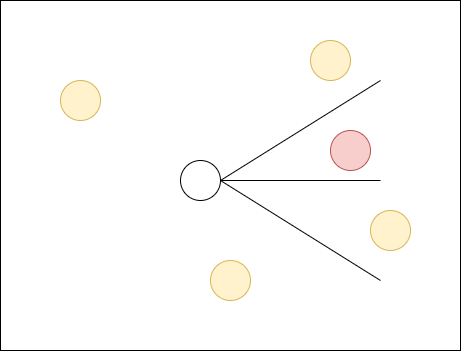
Detectando objetos que entram dentro do campo de visão do personagem. Útil para servir de "gatilho" para eventos em um jogo.

Desenvolvimento de um sistema de monitoramento que exibi todos os eventos que acontecem na garagem automatizada, como abertura de portões ou ocupação de vagas.

Esperávamos horas para baixar apenas alguns megabytes. Nessas horas, quando o telefone tocava nós fazíamos de tudo para não atender o telefone. Mas infelizmente nem sempre dava certo....

Hoje em dia não é mais necessário gastar o nosso tempo com tarefas que podem se automatizadas. Os robôs estão aqui para nos ajudar...
Ao ser aplicado permite que os detalhes passem a depender de abstrações, respeitando a direção da regra de dependências.
Em português, gestão de portofólio de produto. É uma estratégia de análise utilizada para a distribuição de recursos para um produto ou serviço.
Conjunto de códigos prontos para a utilização no desenvolvimento de softwares, eliminando processos como planejamento de arquitetura de classes.
Método de desenvolvimento em que os testes são a base da implementação. Eficiente para mitigar bugs de forma automática.