Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Postado em 12 março 2023
Atualizado em 12 março 2023
Diversos jogos e aplicativos de navegação usam métodos de inteligência artificial para encontrar o melhor caminho entre dois pontos. Existem diversos métodos de pathfinding existentes com suas vantagens e desvantagens. O quê define se um algoritmo é ideal ou não é o contexto do programa.
Os algoritmos de pathfinding, por exemplo, são ideais para jogos onde o inimigo deve seguir algum objeto ou encontrar o menor trajeto até um certo ponto, desviando de obstáculos. Esse projeto aborda sobre o algoritmo A* em um plano bidimensional (2D). Tentaremos encontrar o melhor caminho entre dois pontos usando o algoritmo A* dentro de um labirinto com caminhos estreitos.
Essa demonstração será desenvolvida em p5, usando a linguagem de programação javascript. O ambiente utilizado para rodar o programa será o próprio editor do p5.
O labirinto será construído com um array bidimensional pré-definido de zeros (0) e uns (1). Os zeros representarão caminho livre para deslocamento e os uns representarão as paredes. Veja abaixo um pequeno exemplo:
let map = [
[0, 1, 1, 1, 0, 1],
[0, 0, 1, 0, 0, 1],
[1, 0, 0, 0, 1, 1],
];
O deslocamento da posição do quadrado será feito somente na vertical e horizontal. O deslocamento na diagonal não será realizado.
A fórmula para calcular o melhor caminho também será adotada no algoritmo.
A letra “g” é o caminho percorrido e a letra “h” é o caminho que falta percorrer para chegar ao destino. O “f” é o resultado da soma dos custos para chegar ao destino. Por isso, quanto menor for o “f”, melhor o caminho.
Para calcular o “h” da fórmula acima, é necessário usar outra fórmula. A fórmula usada para calcular a heurística (h) será a distância euclidiana, cuja fórmula também considera valores na diagonal, trazendo resultados bastante satisfatórios.
O x2 e o y2 representam as coordenadas do destino. O x1 e o y1 representam as coordenadas do ponto de origem.
Será implementada uma classe chamada “Node” que será especializada em instanciar os valores de heurísticas, coordenadas e parentes de cada bloco. A variável responsável por gerenciar esses “nodes” será a lista aberta, que terá escopo global. Todos os elementos dentro da lista aberta serão calculados. Uma vez que um elemento é calculado, ele é removido da lista e adicionado à lista fechada, que é outra variável com escopo global, responsável por gerenciar os blocos que já foram calculados, prevenindo a repetição de cálculos de blocos que já foram calculados. Caso a lista aberta torne-se vazia e o bloco destino não seja encontrado, o algoritmo finaliza automaticamente, dando a entender que o destino não é acessível e não foi encontrado.
Antes de começar a escrever os algoritmos, definiremos as constantes básicas do programa.
const SW = 620; // 20*31 Largura do canvas
const SH = 420; // 20*21 Altura do canvas
const X_LENGTH = 31; // Número de elementos em cada linha do mapa
const BS = 20; // Tamanho do bloco
O mapa do jogo será definido com 31 elementos na horizontal (coluna) e 21 elementos na vertical (linha). A largura e a altura do canvas é o resultado da multiplicação das linhas e das colunas com a constante “BS”.
O mapa é um labirinto de zeros e uns. O labirinto abaixo será usado como mapa:
const MAZE = [
[0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, ],
[1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, ],
[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, ],
[1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, ],
[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, ],
[1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, ],
[1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, ],
[1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, ],
[1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, ],
[1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, ],
[1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, ],
[1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, ],
[1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, ],
[1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, ],
[1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, ],
[1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, ],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, ],
[1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, ],
[1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, ],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, ]
]
Em seguida, cria-se as seguintes váriaveis:
var closedList = []; // Lista fechada
var openList = []; // Lista aberta
var isFinished = false; // Flag do a*
As variáveis acima terão escopo global e poderão ser acessadas de qualquer local. A variável “isFinished” definirá se a busca foi finalizada ou não.
Seguindo adiante, teremos que desenvolver as seguintes funcionalidades:
A palavra “node” pode ser traduzida para “nó” e representa um quadrado no labirinto. Cada quadrado terá coordenada de posição, valores de heurística e parente para encontrar o caminho de volta para o ponto inicial após encontrar o ponto de destino.
class Node {
constructor(parentNode, pos, g, h) {
this.id = calculateId(pos); // Define id com base na posição
this.parentNode = parentNode; // Parente node
this.pos = pos; // Coordenadas
this.g = g; // Custo até o momento
this.h = h; // Expectativa de custo no futuro
this.f = g + h; // Melhor custo
}
}
Lembrando que quanto menor o “f”, menor é o custo de um ponto até o outro.
A função setup é de domínio da biblioteca p5. Nessa função inicializamos as instâncias necessárias.
function setup() {
// Exibi o canvas na tela
createCanvas(SW, SH);
// Inicializa a lista fechada
for (let row = 0; row < MAZE.length; row++) {
closedList[row] = [];
for (let column = 0; column < MAZE[row].length; column++) {
closedList[row][column] = false;
}
}
// Cria o ponto de início
initNode = new Node(null, createVector(2, 2), 0, 0);
// Cria o ponto atual, para referência no mapa
currentNode = new Node(null, initNode.pos.copy(), 0,0);
// Inseri ponto inicial na lista aberta
openList.push(initNode);
}
A lista fechada é responsável por gerenciar os blocos já calculados. Quando um bloco é calculado e inserido na lista fechada, ele passa a ser ignorado, pois não há mais necessidade de calcular novamente um bloco já calculado. No começo, todos os blocos são falsos (ainda não calculados).
O processo de exibição do mapa na tela é bastante parecido com a inicialização da lista fechada. Dentro da função “draw”, invocamos a função “drawMaze”, que irá exibir um bloco. Para exibir todos os blocos, colocamos a função “drawMaze” dentro de um loop bidimensional.
function draw() {
// Cor do canvas
background(0, 0, 0);
for (let row = 0; row < MAZE.length; row++) {
for (let column = 0; column < MAZE[row].length; column++) {
// Exibi o bloco na coordenada row x column
drawMaze(row, column)
}
}
...
}
A função “draw” também é de domínio do p5. Essa função é executada infinitamente. Dentro da função “drawMaze”, escrevemos o seguinte código:
function drawMaze(row, column) {
// Desenha bloco (Branco)
if (MAZE[row][column] == 1) {
fill(color(255, 255, 255));
square(column * BS, row * BS, BS);
}
// Node de destino (Vermelho)
if (column == destNode.pos.x && row == destNode.pos.y) {
fill(color(255, 0, 0));
square(destNode.pos.x * BS, destNode.pos.y * BS, BS);
}
// Node de início (Verde)
if (column == initNode.pos.x && row == initNode.pos.y) {
fill(color(0, 255, 0));
square(initNode.pos.x * BS, initNode.pos.y * BS, BS);
}
}
Caso a coordenada atual tenha o valor 1, exibimos a parede como obstáculo, cujo obstáculo será representado com um bloco de cor branca. Caso a coordenada atual tenha o valor 0, simplesmente não desenhamos nada. O ponto inicial é representado por um bloco verde e o ponto destino é representado pelo bloco vermelho.
Se tudo ocorrer como esperado, teremos o resultado abaixo:

O algoritmo A* é a parte principal do programa. Ele irá examinar todas as possibilidades dos melhores caminhos do ponto de início até o ponto de destino.
Lembrando que a biblioteca p5 tem a função “draw” que se repete infinitamente. Iremos adaptar o algoritmo A* para rodar no contexto do p5.
Primeiramente, começamos definindo a função “aStar()”:
function aStar() { }
Dentro da função, verificamos se a lista aberta ainda tem elementos dentro dela, caso contrário, o programa terá que ser finalizado.
if (openList.length == 0) {
isFinished = true;
return;
}
Em seguida, pegamos o índice do Node dentro da lista aberta que está mais perto do destino. Para fazer isso, basta descobrirmos o Node com o menor “f”,
let lowestIndex = 0;
for (let i = 0; i < openList.length; i++) {
if (openList[i].f < openList[lowestIndex].f) {
lowestIndex = i;
}
}
Retiramos o elemento da lista aberta com o índice encontrado e adicionamos à lista fechada com antecedência, pois iremos calcular o bloco atual logo em seguida.
const firstElement = openList.splice(lowestIndex, 1);
currentNode = firstElement[0];
closedList[currentNode.pos.y][currentNode.pos.x] = true;
Antes de começar a calcular o bloco, nos certificamos se chegamos ou não no destino.
if (currentNode.pos.x == destNode.pos.x && currentNode.pos.y == destNode.pos.y) {
isFinished = true;
return;
}
Se não tivermos chegado ainda no destino, pesquisamos os vizinhos do bloco atual para descobrir qual é o bloco que está mais perto do destino. Isso é feito checando os blocos na horizontal e vertical, nos sentidos norte, sul, oeste e leste.
// Blocos vizinhos
let directions = [];
// Leste
directions[0] = createVector(currentNode.pos.x + 1, currentNode.pos.y);
// Oeste
directions[1] = createVector(currentNode.pos.x - 1, currentNode.pos.y);
// Norte
directions[2] = createVector(currentNode.pos.x, currentNode.pos.y - 1);
// Sul
directions[3] = createVector(currentNode.pos.x, currentNode.pos.y + 1);
Após definirmos as coordenadas dos blocos vizinhos, entramos na lógica principal do algoritmo A*.
for (let i = 0; i < directions.length; i++) {
// Não é parede, não é limite da tela e não está presente na lista fechada
if (isValid(directions[i])) {
// Custo atual
const g = currentNode.g + 1;
// Expectativa de custo até o destino
const h = euclideanDistance(directions[i]);
// Node do bloco vizinho
const newNode = new Node(currentNode, directions[i], g, h);
// Se node já existe na lista aberta, obtemos o seu índice
const index = openListContainsNode(newNode);
if (!index) {
// Caso ainda não exista na lista aberta, adicionamos
openList.push(newNode);
} else if (index && openList[index].f > newNode.f) {
// Caso exista na lista aberta, mas tem um custo menor do que o existente remove e adiciona novamente com um novo parente
openList.push(newNode);
openList.splice(index, 1);
}
}
};
As 4 direções serão calculadas dentro do loop. Caso a direção seja parede, esteja fora dos limites do mapa ou esteja incluída na lista fechada, ela é ignorada. No momento que instanciamos a variável “newNode”, já temos o “f” calculado. Após isso, verificamos se o node existe na lista aberta baseando-se na sua coordenada x e y no mapa. Caso o node ainda não exista na lista aberta, adicionamos. Caso o node já exista na lista aberta, mas tem um custo menor do que o atual, substituímos o existente com um parente novo.
Cada node terá um parente node. Os parentes são necessários para que possamos encontrar o caminho de volta para o início após encontrarmos o destino.
Como mostra acima, isso nos possibilita encontrar a origem de volta para o início através da corrente de parentes formada.
A expectativa de custo é calculada com a heurística da distância euclidiana:
function euclideanDistance(pos) {
return sqrt(sq(destNode.pos.x - pos.x) + sq(destNode.pos.y - pos.y));
}
A função “openListContainsNode” verifica se o “newNode” já existe na lista aberta usando a propriedade “id” que é baseada nas coordenadas do Node.
function openListContainsNode(targetNode) {
let nodeIndex = openList.findIndex(function(node, index) {
return node.id == targetNode.id;
});
if (nodeIndex == -1) {
return null;
}
return nodeIndex;
}
Simplesmente verificamos se a lista aberta possui um elemento com “id” igual ao que estamos procurando. Caso não encontre, “null” será retornado. Caso encontre, o índice é retornado.
Para calcular o “id” dos nodes, convertemos o vetor (x, y) em um valor linear. Assim o maior valor linear será a largura do mapa multiplicada pela altura do mapa.
A fórmula para a conversão é a seguinte:
function calculateId(pos) {
return (pos.y * X_LENGTH) + pos.x;
}
X_LENGTH é a constante definida ainda no começo desse projeto. Ela tem um valor de 31, que é o número de elementos presentes em uma linha na horizontal. Na fórmula acima, caso estejamos em um coordenada x = 15 e y = 10, teremos id = 325.
Dentro da função “isValid”, verificamos os obstáculos e a lista fechada:
function isValid(direction) {
if (direction.x > ((SW / BS) - 1) || direction.x < 0 || direction.y > ((SH / BS) - 1) || direction.y < 0) {
return false;
}
if (inClosedList(direction) || isWall(direction)) {
return false;
}
return true;
}
Para testar o resultado, precisamos fazer algumas implementações adicionais. Como blocos que representam a lista fechada, bloco atual e o caminho mais curto encontrado. Para exibir o bloco atual e a lista fechada na tela, basta adicionarmos blocos coloridos na função “drawMaze”.
// Lista fechada (Azul)
if (closedList[row][column]) {
fill(color(0, 0, 255));
square(column * BS, row * BS, BS);
}
// Bloco atual (Amarelo)
if (column == currentNode.pos.x && row == currentNode.pos.y) {
fill(color(255, 255, 0));
square(currentNode.pos.x * BS, currentNode.pos.y * BS, BS);
}
Em seguida, adicionamos uma função para obter o caminho mais perto obtido através dos parentes. Também definiremos uma nova array bidimensional com escopo global para armazenar as coordenadas dos parentes.
var closestPath = [];
Faremos a mesma coisa que a lista fechada e o bloco atual, adicionando a cor dos quadrados do caminho com menos custo.
// Bloco de parentes (Vermelho)
if (closestPath[row][column]) {
fill(color(255, 0, 0));
square(column * BS, row * BS, BS);
}
Em seguida, preenchemos a array acima com os parentes da variável “currentNode” após encontrarmos o bloco destino.
var currentParentNode = currentNode.parentNode;
while (currentParentNode != null) {
closestPath[currentParentNode.pos.y][currentParentNode.pos.x] = true;
currentParentNode = currentParentNode.parentNode;
}
A porção de código acima pode ser inserida dentro da condição da função “aStar” logo após encontrarmos o ponto destino. Se tudo ocorrer conforme o esperado, teremos o resultado abaixo:
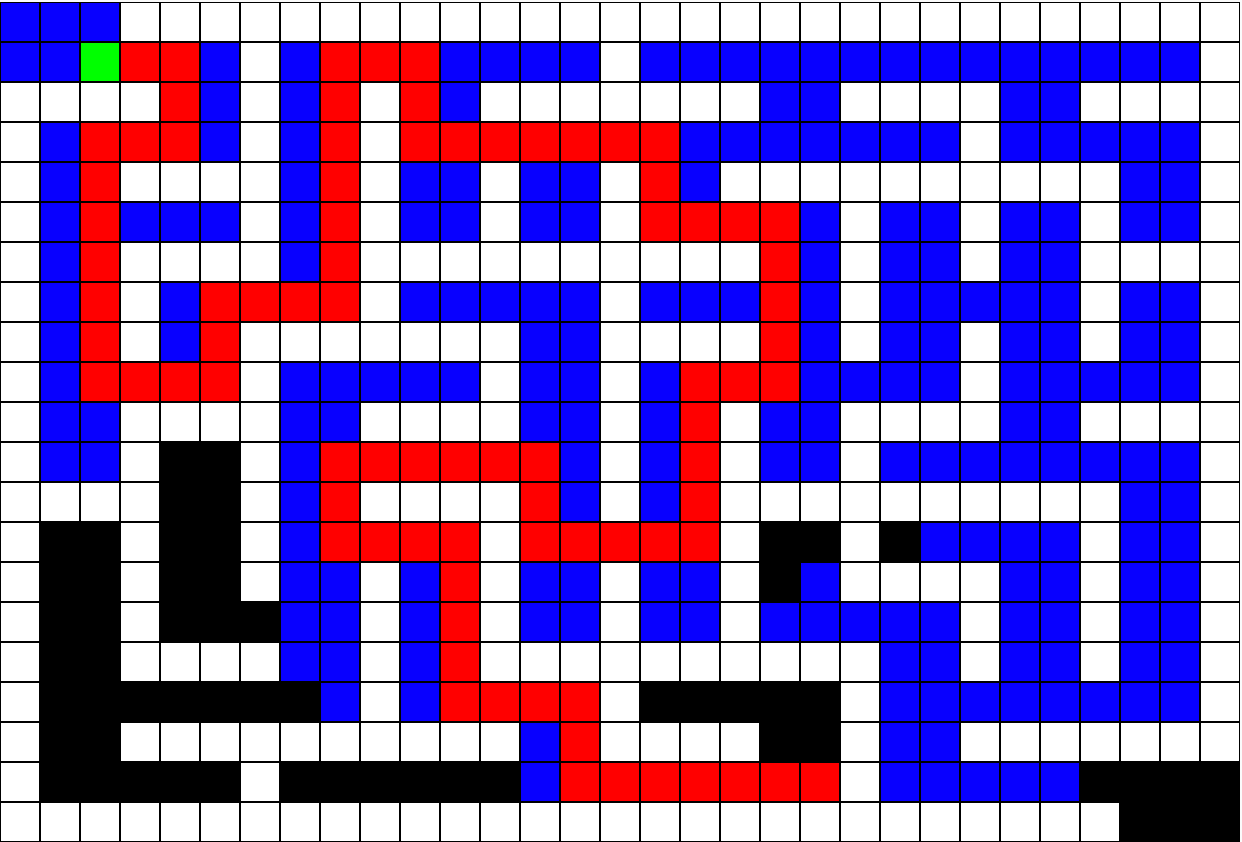
Existem muitos outros algoritmos de pathfinding, porém o algorimo A* é um dos mais usados, devido a sua eficiência de encontrar o melhor caminho sem desperdício. Nesse projeto, o nosso contexto foi um simples labirinto definido em um array bidimensional contendo zeros e uns. Porém, em outros contextos o algoritmo pode sofrer diversas modificações para melhor adaptação e integração do ambiente.
O resultado final está disponível no editor do p5.
https://editor.p5js.org/Dicionariotec/sketches/RTC49W4F0
Postagens mais vistas

Os 5 principais componentes do computador são a unidade de controle, unidade aritmética e lógica, memória, dispositivo de entrada e dispositivo de saída.
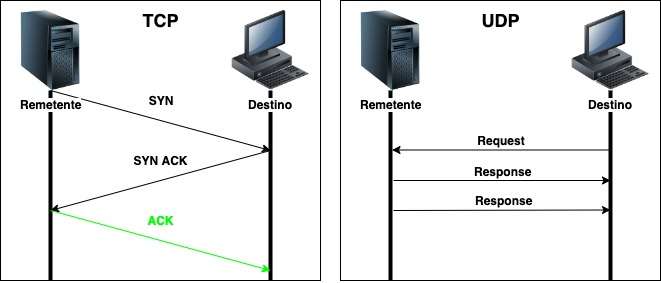
A porta é um número de 16 bits que é adicionado no final do endereço IP, insinuando qual aplicativo está vinculado e atuando nessa porta.
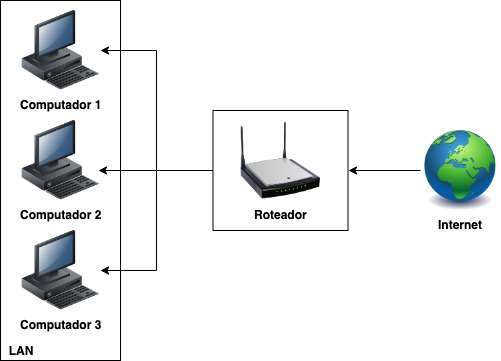
Rede local de computadores (LAN) é um conjunto de computadores ou dispositivos conectados uns aos outros de forma isolada em um pequeno local.