Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Categoria de Programação
Postado em 09 março 2023
Atualizado em 09 março 2023
Palavras-chave: algoritmo,busca,linear,binario,binaria,estrela,asterisco,aplicativo,distancia,caminho,calculo
Visualizações: 6125
O contexto que um programa de computador roda, afeta diretamente o tipo de algoritmo que será implementado. Uma simples tarefa como a busca de algum elemento dentro de uma lista pode ser realizada usando métodos de busca linear. Porém, programas que necessitam de mais eficiência podem optar pela busca binária.
Conforme o contexto do programa muda, os algoritmos precisam ser adaptados. Em aplicativos de navegação ou em jogos, algoritmos de busca também são implementados para encontrar o caminho mais curto entre dois objetos, como a distância atual do usuário até um determinado objeto. Um algoritmo bastante eficiente para encontrar o menor caminho entre dois pontos é o algoritmo A*.
O algoritmo A-estrela é um método que busca o caminho mais curto entre dois pontos. Esse método usa os valores de duas funções para estimar o melhor caminho em relação ao custo, cujos valores são o G e o H.
A soma dos dois valores acima estimam o caminho mais eficiente de um ponto inicial até o ponto final. O resultado dos valores acima é representado com a letra F e quanto menor for esse valor, menos custoso será o trajeto calculado.
O algoritmo A* é considerado um algoritmo inteligente, uma vez que ele pode encontrar o seu destino automaticamente sem a intervenção humana. A eficiência desse algoritmo é bastante relativo, tendo o seu desempenho diretamente influenciado pelo contexto do programa, com fatores como a qualidade dos dados de entrada e os métodos heurísticos adotados. Alguns métodos heurísticos utilizados com frequência são a distância de Manhattan e a distância euclidiana. Geralmente, o método heurístico é usado para estimar o menor valor possível até o destino do objeto.
O algoritmo A* pode ser usado em exercícios de grafos ou mapas para calcular a menor distância entre dois pontos. Esse algoritmo pode ser usado em jogos, aplicativos de navegação e em robôs.
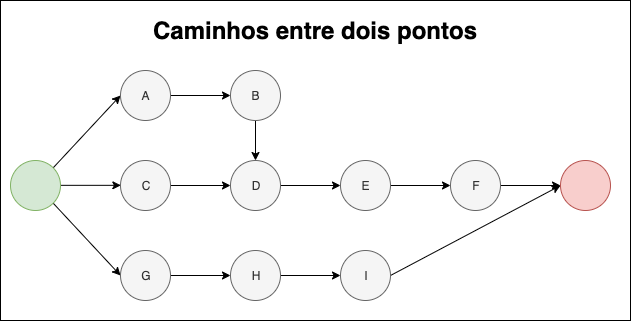
No exemplo acima, seguindo a ordem das setas, teríamos 3 opções de caminhos até o ponto final (ponto vermelho). Sem nenhum cálculo é possível perceber que o caminho mais curto é o G, H, I. Porém, o método A* pode ser usado em problemas muito mais complexos, contendo muito mais valores complexos a serem considerados do que o exemplos acima.
Um labirinto 2D é um bom candidato para ter um algoritmo A* implementado. Um labirinto, geralmente possui diversos obstáculos e caminhos sem saída até chegar ao seu destino final.

Na imagem acima, temos um labirinto 2D, onde cada cor tem uma representação:
É possível perceber que no exemplo acima, os valores na diagonal também são calculados. O labirinto acima possui ao todo 651 quadrados (31x21). O total de quadrados que tiveram que ser calculados até podermos estimar o menor caminho até o destino foi de 247 quadrados. Isso é apenas 37% do total de quadrados. Sendo que 44% (291 quadrados) do labirinto é composto de paredes e 56% (360 quadrados) do labirinto é composto por quadrados pretos (caminho com possibilidade de locomoção), podemos chegar a conclusão que apenas 68% dos quadrados pretos foram necessários para estimar o melhor caminho até o destino, o que é bastante eficiente para um labirinto com caminhos estreitos. Mas o que aconteceria se não tivéssemos paredes? Veja o resultado abaixo:

O exemplo acima possui um mapa de 651 quadrados (31x21) e não contém paredes. A quantidade total de quadrados que precisaram ser calculados para estimar o menor caminho foi 19 quadrados, ou seja, 2.9% de quadrados em relação ao mapa. Assim, podemos chegar a conclusão que o algoritmo A* é bastante eficiente. Porém, em mapas complexos contendo obstáculos, ele tem uma notação de O(n), onde o “n” é a quantidade de quadrados a serem calculados.
A aplicação do algoritmo A* pode variar dependendo do contexto do programa. Um dos métodos que mais podem variar é o método de heurística, usado para calcular a distância do ponto atual até o ponto final. A fórmula para calcular o melhor caminho do ponto atual até o destino é:
Onde o “g” é o caminho total percorrido até o ponto atual e o “h” é a heurística do ponto atual até o destino. O “f” é o custo total estimado do ponto atual até o destino.
Geralmente, o algoritmo A* usa duas variáveis para gerenciar o programa:
A lista aberta contém pontos (coordenadas) que ainda não tiveram o seu melhor custo calculado. Dependendo do caminho do início até o ponto atual, ainda podem haver rotas com menores custos até o destino final. Pontos que ainda precisam ser calculados, estarão situados dentro da lista aberta.
Os pontos dentro da lista aberta terão o seu custo calculado através dos seus pontos vizinhos. O algoritmo testa todas as direções possíveis a partir do ponto atual, se locomovendo um intervalo a frente (x + 1 ou y + 1 em espaços 2D) e calculando a heurística para chegar ao ponto final. A direção que apresenta menor heurística será escolhida e adicionada à lista aberta com o ponto atual como parente.

A lista fechada contém objetos que já tiveram todos os seus vizinhos calculados. Os objetos inseridos na lista fechada são interpretados como concluídos ou custosos e ineficientes. Uma vez que a coordenada é inserida na lista fechada, ela passa a ser ignorada, fazendo com que a lista aberta continue avançando até chegar ao destino final.
O algoritmo A* pode variar dependendo do contexto e das técnicas adotadas. Um dos diversos exemplos de algoritmo A* que existem é o abaixo:
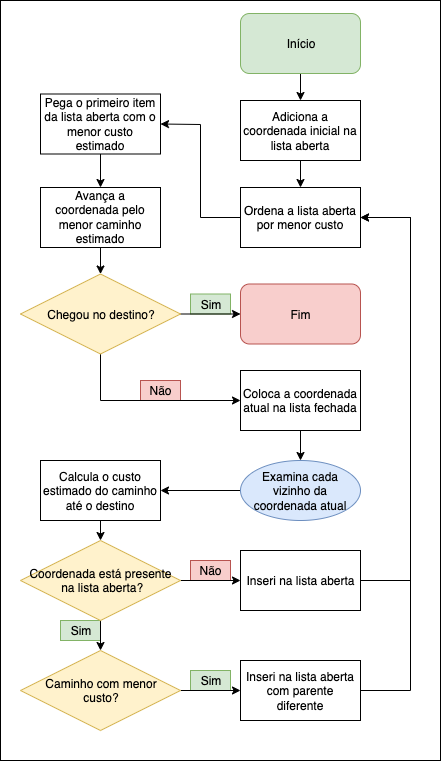
As etapas do algoritmo acima em detalhes são:
O algoritmo A* é uma técnica de busca do menor caminho possível entre o ponto inicial e o destino. Esse método pode ser implementado tanto em simples problemas até em problemas complexos. Esse algoritmo é considerado como parte do campo de inteligência artificial de sistemas de busca inteligente.
Projetos práticos

Convertendo imagens para ascii art usando o valor da intensidade das cores cinzentas.
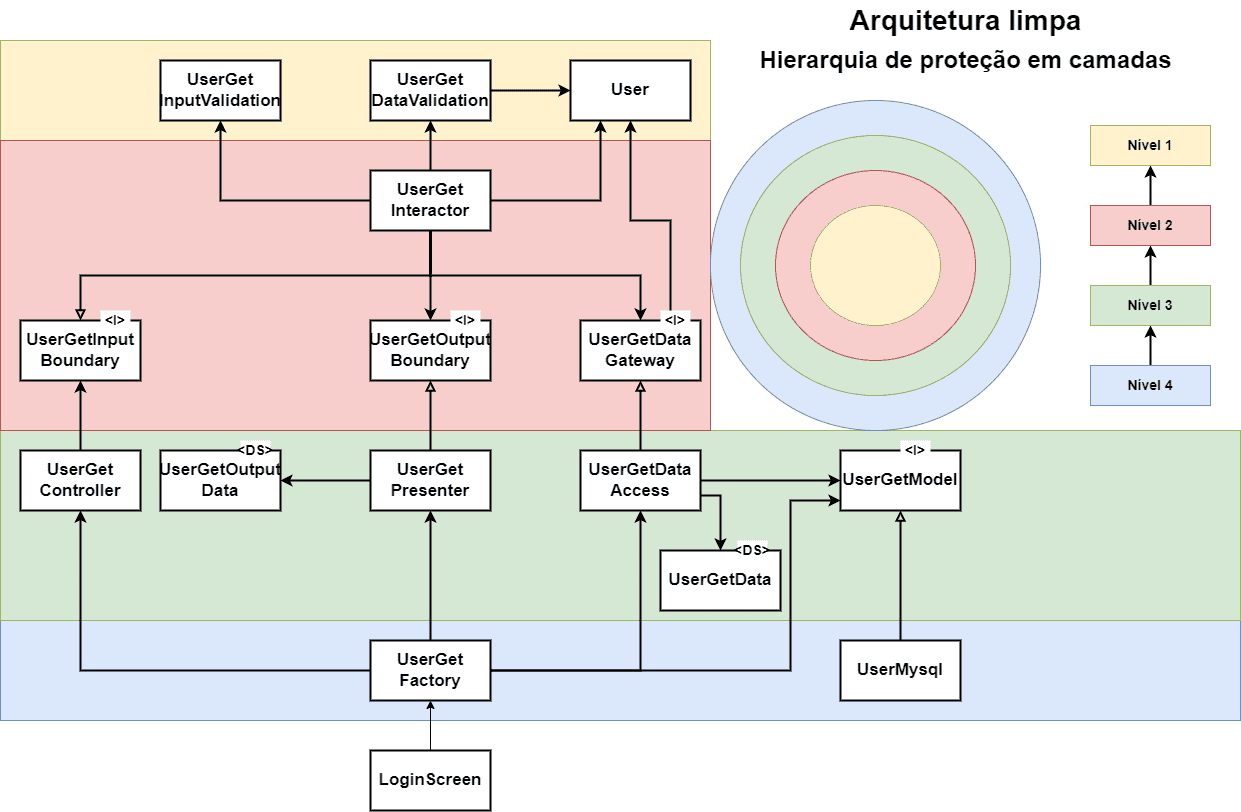
Usando JavaFX e arquitetura limpa para criar um aplicativo de caixa eletrônico extremamente simples.
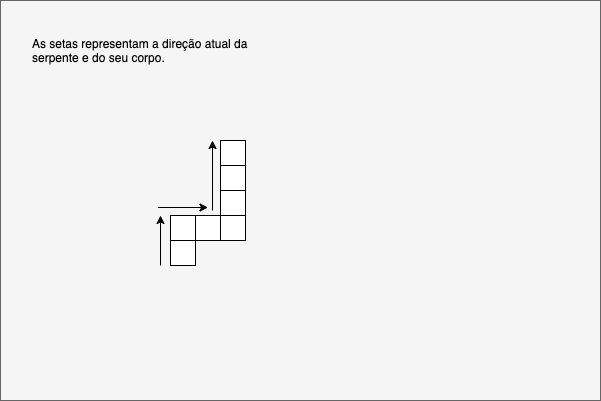
Programando o clássico jogo da serpente usando o framework p5.js. Tutorial indicado para iniciantes da programação que querem aprender os conceitos básico da área criando jogos.
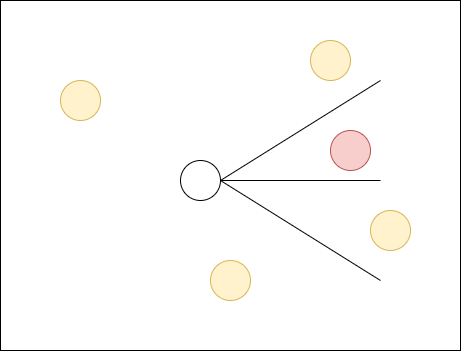
Detectando objetos que entram dentro do campo de visão do personagem. Útil para servir de "gatilho" para eventos em um jogo.
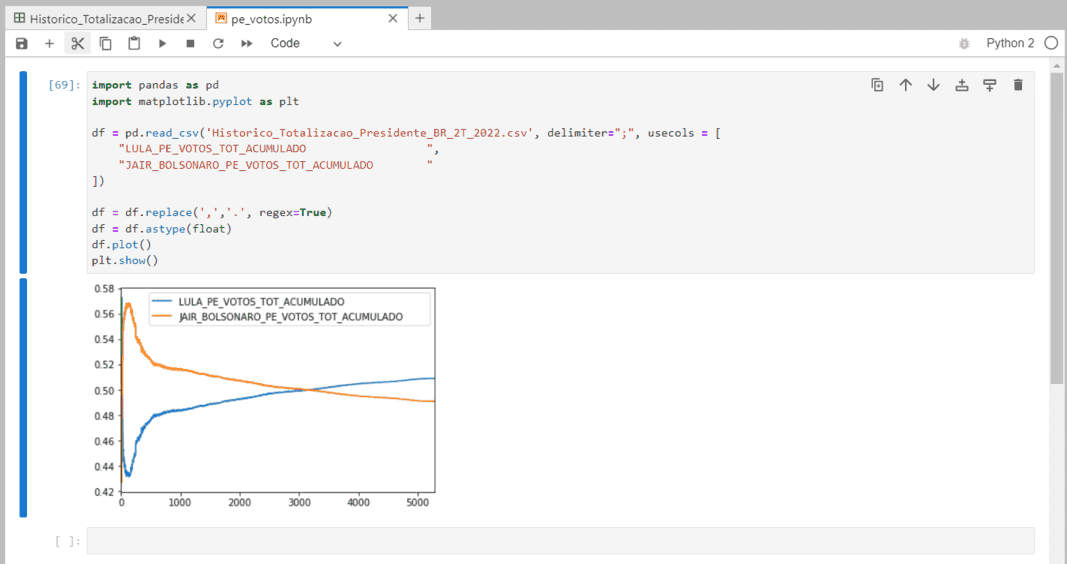
Simulação dos gráficos do segundo turno das eleições presidenciais, utilizando python e ferramentas de análise de dados, pandas e jupyter.

O envenenamento de cache DNS redireciona o usuário para um site falso, mesmo digitando um URL legítimo. Como isso é possível??!!

As criptomoedas mudaram totalmente o modo das pessoas pensarem. Usar robôs para autentificar transações online, custa muito menos comparado com os bancos em relação às taxas...
Três tipos de comportamentos usados em steering behaviors para simular comportamentos de seres vivos de forma realística.
A busca linear é um algoritmo de força bruta não muito eficiente, mas com grande simplicidade, sendo utilizada regularmente por programadores.
Subcampo da inteligência artificial inspirado no sistema de neurônios de seres inteligentes como o dos humanos, permitindo com que as máquinas aprendam.
Conjunto de técnicas de algoritmo que simulam comportamentos realísticos. Usado em jogos e em pesquisas biológicas para o estudo de comportamentos.