Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Categoria de Tecnologia
Postado em 15 março 2023
Atualizado em 15 março 2023
Palavras-chave: fpu,cpu,agu,computador,componente,calculo,matematica,notacao,cientifica
Visualizações: 3020
Em meados dos anos 80, os processadores ainda enfrentavam desafios para realizar cálculos de aritmética com números que possuem vírgula. Nessa época, a unidade de ponto flutuante (FPU) era um componente opcional e separado do processador. Computadores que possuíam um FPU, passavam a ser chamados de computadores científicos.
Mesmo sem a presença de um FPU, os computadores ainda podem realizar cálculos de aritmética de números com vírgula. Usando softwares que simulam o funcionamento do FPU, instruções podem ser implementadas em nível de linguagem de programação. Porém, a velocidade do cálculo não é tão veloz e o resultado final não é muito preciso. Por essa razão, ter um componente em nível de hardware especializado em cálculos aritméticos de números com vírgula é essencial para a máquina ter um bom desempenho. Hoje, raramente existem computadores sem uma FPU integrada ao processador.
A unidade de ponto flutuante (FPU), em inglês “floating-point unit”, é um componente hardware especializado em realizar cálculos de números com vírgula. Esse componente começou a ser usado em computadores residenciais no ano de 1989, após o lançamento do Intel i486. Como referenciado no livro GAME ENGINE BLACK BOOK DOOM, a ausência da unidade de ponto flutuante era um grande problema para os computadores da época. Jogos como o DOOM, usavam a aritmética de ponto fixo para calcular a distância aproximada entre dois pontos.
O Intel i486 foi um marco importante no mercado de computadores pessoais, processadores passaram a calcular com mais precisão graças ao FP (floating-point), o que permitiu que cálculos de terceira dimensão (3D) pudessem ser realizados, contribuindo para o desenvolvimento de jogos e aplicativos inovadores na época.
Pelo fato da máquina trabalhar com a numeração binária, a representação dos números decimais acompanhados com vírgula apresenta problemas como falta de bits (número de dígitos não é suficiente). Por isso, a representação adotada pelos computadores é a notação científica.
Os computadores usam a notação científica para representar a posição da vírgula em um valor. Esse valor, em decimal pode ser processado usando o seguinte modelo:
Assim, tendo um valor mais preciso e aproveitando melhor o uso dos bits.
A aplicação do modelo acima, pode ser realizado da seguinte maneira: Imagine que temos o valor decimal abaixo e queremos processar essa informação.
O valor acima é de 5 bilhões. Usando a notação científica, podemos mudar a expressão.
Repare como é mais fácil de manipular o número acima usando notação científica. O valor foi divido em três elementos: mantissa (5), base (10) e expoente (9). Também é possível aplicar em números abaixo de zero:
Levando em consideração que os valores são gravados e processados em bits, diminuir o número de dígitos sem modificar o valor ajuda a economizar espaço. Os valores podem ser processados usando o formato float ou double, cujos formatos respectivamente podem representar o valor com 32 bits ou 64 bits. Como mostrado no exemplo acima, o computador normaliza o valor da mantissa do valor fracionário, deslocando a vírgula para a direção direita quando positivo e para esquerda quando negativo. Quando o número é menor do que zero, ele tem o expoente negativo e quando é maior do que dez, o expoente é positivo.
Diferente dos humanos, a máquina processa as informações usando números binários. Por essa razão os cálculos devem ser realizados usando binários.
Imagine o seguinte valor de 43,167.
Para calcular o valor acima usando números binários, primeiro temos que segmentar o número antes da vírgula e transforma-lo em binário. Lembrando que para converter um número decimal em binário, temos que dividir essa número até ele chegar a zero e memorizar a sobra em cada divisão.
Na ordem de baixo para cima, juntamos os zeros e uns para ter o resultado final do número binário que é 101011. Em seguida, convertemos o valor após a vírgula em número binário, mas diferente da resolução acima, os números depois da vírgula serão multiplicados por 2 e serão marcados como sobra caso ultrapassem o 1.
Quando um dos valores se repetem, podemos parar a multiplicação. Diferente dos números antes da vírgula, os números depois da vírgula tem as suas sobras juntadas de cima para baixo: 00101.
No final temos um valor binário de .
Em seguida precisamos aplicar a notação científica no resultado. Normalizamos a mantissa do valor deslocando a vírgula para a esquerda 5 casas e escrevemos o expoente:
O resultado acima, em um formato float de 32 bits terá os seguintes aspectos:
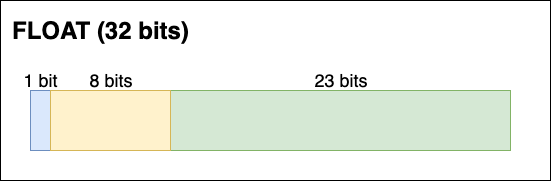
A unidade de ponto flutuante é um componente capaz de fazer cálculos aritméticos usando a notação científica. A vírgula flutuante permite que a máquina possa obter resultados mais precisos, possibilitando o desenvolvimento de aplicativos e jogos que necessitam de precisão e eficiência no processamento de números complexos.
Projetos práticos

Desenvolvimento dos conceitos mais básicos do clássico pacman, como: mapa, animação, deslocamento e detector de colisões.
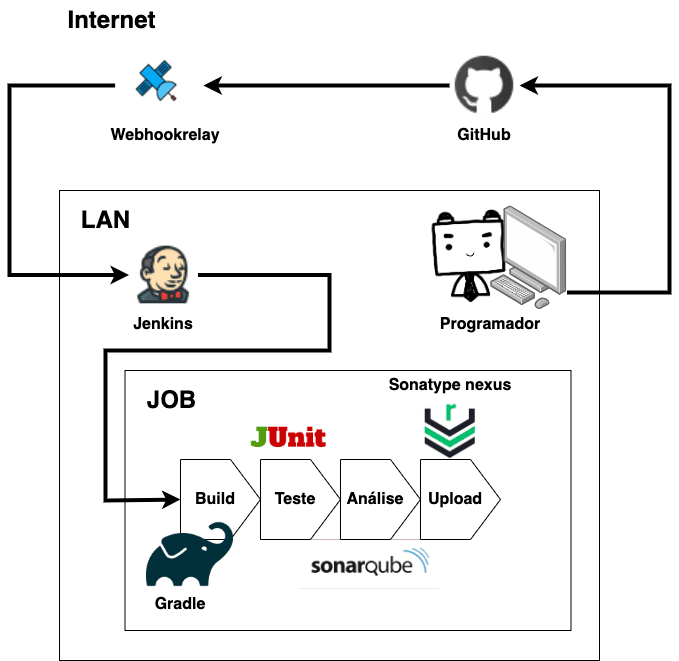
Fazendo a integração contínua de Jenkins, Sonatype Nexus, Sonatype, JUnit e Gradle para automatizar processos repetitivos. Prática bastante usada em tecnologias de DevOps.

Projeto de comunicação entre dois dispositivos ESP8266 e Raspberrypi4. Laravel irá funcionar como servidor e receptor de dados de temperatura e umidade coletados com o DHT11.
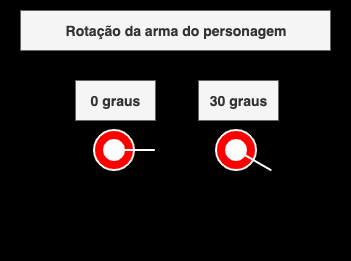
Usando lógicas matemáticas como trigonometria para criar e calcular o esqueleto de um jogo de tiro 2D em javascript
Programando um jogo clássico de arcade usando javascript e p5.js. O usuário deve quebrar os blocos utilizando uma bola ao mesmo tempo que evita que a bola saia pela parte inferior da tela

Expressões como gastar tempo e investir tempo andam lado a lado. Quando algo investido não tem o retorno esperado isso se torna uma perde de tempo...

A engenharia social é a forma mais fácil de roubar os dados da vítima, principalmente aqueles que não estão antenados..
Data Science ou ciência de dados, é uma área de computação que se concentra em extrair informações valiosas de grandes quantidades de dados.
Conjunto de dados armazenados temporariamente na placa de vídeo em forma de matriz. Esses dados serão usados para exibir os frames na tela do monitor.
Caracterizam uma grandeza física que possui módulo, direção e sentido. Pode simular eventos como queda, atração e deslocamento de objetos em um meio.
O PERT é um método composto por linhas e nós conectados entre si com o intuito de representar a dependência entre as atividades.