Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Esse site utiliza cookies
Nós armazenamos dados temporariamente para melhorar a sua experiência de navegação e recomendar conteúdo do seu interesse.
Ao utilizar os nossos serviços, você concorda com as nossas políticas de privacidade.
Postado em 19 fevereiro 2023
Atualizado em 19 fevereiro 2023
Esse projeto mostra os cálculos trigonométricos utilizados em jogos de tiro 2D visto de cima. Diferente de um jogo de RPG, um jogo de tiro usa a rotação do personagem para facilitar o foco da arma.
Esse projeto é apenas um esqueleto de um jogo. Os pontos principais desse projeto são os cálculos trigonométricos que são de extrema importância para a rotação e movimentação do personagem.
Os conceitos abordados serão:
Nesse esqueleto, o personagem poderá ser controlado apenas pelo teclado, através das setas “cima”, “baixo”, “esquerda” e “direita”. As teclas “esquerda” e “direita” são usadas para rodar o ângulo do personagem, enquanto as teclas “cima” e “baixo” são usadas para avançar e recuar. O personagem também poderá atirar apertando a tecla “espaço”. A detecção de colisões pode fazer a checagem de conflito entre a parede e o personagem, assim como os tiros e as paredes.
A biblioteca P5.js será usada nesse projeto. O editor selecionado será o próprio editor disponibilizado pelo P5.js. O projeto completo pode ser acessado no link abaixo:
Resultado final (link externo)
A biblioteca P5 usa apenas duas funções: “setup” e “draw”. O “setup” é chamado apenas uma vez ao executar o programa e a função “draw” é chamada repetidamente.
Primeiro iniciamos definindo o tamanho da tela.
const SCREEN_HEIGHT = 480;
const SCREEN_WIDTH = 480;
A altura e o comprimento da tela serão iguais, com o valor de 480. Esses valores serão usados para definir o tamanho do canvas, onde todos os objetos do jogo serão exibidos. Na função “setup”, criamos o canvas:
createCanvas(SCREEN_WIDTH, SCREEN_HEIGHT);
O mapa será armazenado em um array multidimensional. Os elementos do array serão compostos por zeros e uns, onde zero (0) representa caminho vazio e um (1) representa parede.
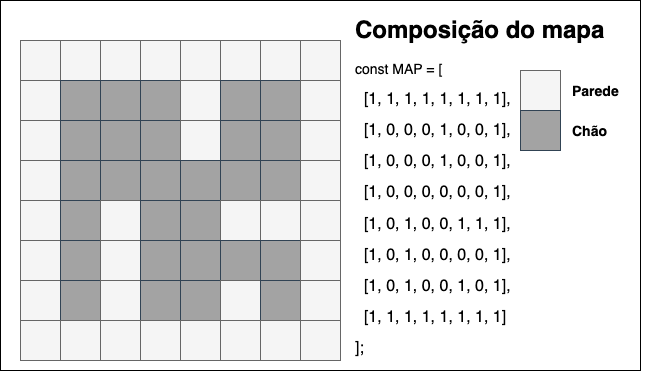
O array acima será usado para exibir o mapa e fazer a fazer a detecção de colisões posteriormente. A lógica do algoritmo da exibição mapa está escrito na função “drawMap”, cuja função será chamada na função “draw”.
function drawMap() {
for (let rowIndex = 0; rowIndex < MAP.length; rowIndex++) {
// Altura da tela é 480 e o tamanho do array do mapa na vertical é 8
let tileSizeY = SCREEN_HEIGHT / MAP.length;
for (let colIndex = 0; colIndex < MAP[rowIndex].length; colIndex++) {
// Comprimento da tela é 480 e o tamanho do array do mapa na horizontal é 8
let tileSizeX = SCREEN_WIDTH / MAP[rowIndex].length;
// Caso seja parede, o bloco é pintado com a cor cinza
if (MAP[rowIndex][colIndex] == IS_WALL) {
fill(GREY);
rect(colIndex * tileSizeX, rowIndex * tileSizeY, TILE_SIZE);
continue;
}
// Caso seja chão, o bloco é pintado com a cor preta
fill(BLACK);
rect(colIndex * tileSizeX, rowIndex * tileSizeY, TILE_SIZE);
}
}
}
Pelo fato do array do mapa ser multidimensional, usamos duas loops (repetições). A primeira representa a linha e a segunda representa a coluna. Uma vez que invocamos a função “drawMap” dentro da função “draw”, temos o mapa desenhado na tela.
function draw() {
drawMap();
}
Primeiro, implementamos a classe do personagem. Essa classe possuirá apenas o construtor e a função “draw”. A função “draw” é responsável por exibir o personagem e calcular a rotação da direção que o personagem está apontando.
O personagem será representado por um círculo com um traço representando o local que o personagem está apontando a arma. Os atributos básicos como coordenadas x e y, ângulo e velocidade serão definidos no momento de instanciar a classe do personagem, dentro do construtor.
class Player {
constructor(x, y) {
this.x = x;
this.y = y;
this.scale = 20;
this.angle = 0;
this.speed = 0.25;
}
draw() {
// Exibi o corpo do personagem
stroke(WHITE);
fill(RED);
circle(this.x, this.y, this.scale);
// Exibi a direção da arma e a arma do personagem
let dy = this.y + sin(this.angle) * this.scale;
let dx = this.x + cos(this.angle) * this.scale;
line(this.x, this.y, dx, dy);
// Exibi a cabeça do personagem
fill(WHITE);
circle(this.x, this.y, this.scale / 2);
}
}
Como mostra no construtor, as coordenadas x e y do personagem serão definidas pelos argumentos x e y. A escala (scale) será o tamanho do círculo que representa o personagem. O ângulo é o atributo que armazena o ângulo atual do personagem em radianos. A velocidade (speed) armazena o valor de movimentação e rotação do personagem.
O círculo do personagem é desenhado usando as coordenadas e a escala definidas. Esse círculo vermelho simplesmente exibirá a posição atual do personagem no mapa. As variáveis “dx” e “dy” são usados para exibir a direção atual que a arma do personagem está apontada.
A fórmula utilizada para definir a direção que a arma está apontada funciona com base no ângulo atual do personagem. Considere os seguintes ângulos abaixo, contendo os valores de seno e cosseno:
| - | 30° | 45° | 60° |
|---|---|---|---|
| seno | |||
| cosseno | |||
| tangente | 1 | 3 |
Imagine que o personagem está posicionado no meio da tela com a direção da arma para o ângulo de 30°. Nesse caso, teríamos o seguinte código:
// Instancia o personagem no centro da tela
let player = new Player(SCREEN_WIDTH / 2, SCREEN_HEIGHT / 2);
// Define um ângulo de 30° em radianos (30° * π/180)
player.angle = 30 * PI / 180; // 0.523598775598299
Em seguida, as seguintes fórmulas são usadas para calcular o ponto onde a arma está apontada:
O “dy” e o “dx” são a soma do ângulo atual, multiplicado por 20.
Primeiro, calculamos o valor do dy que é o ponto y do destino da linha na vertical.
Seguindo adiante, calculamos o dx.
Lembrando que no P5, as coordenadas zero do x e do y começam no canto esquerdo na parte superior da tela. Portanto, quando o ângulo do personagem é zero, ele aponta para a direita como mostra na imagem abaixo:
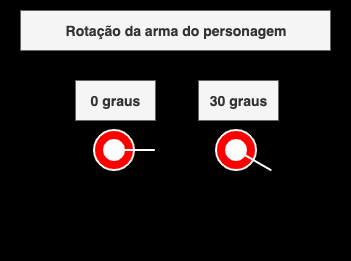
A lógica dos ângulos em relação as coordenadas não são tão complicados quando projetadas em uma tabela. Levando em consideração os ângulos abaixo, quando normalizamos os valores temos a seguinte tabela:
| Ângulo | dx | dy | Direção da arma |
|---|---|---|---|
| 0° | 0 | 1 | Para baixo |
| 90° | 1 | 0 | Para a direita |
| 180° | 0 | -1 | Para cima |
| 270° | -1 | 0 | Para a esquerda |
Sem esquecer que os cálculos de seno e cosseno foram baseadas nas fórmulas de geometria abaixo:
O CO é o cateto oposto e o CA é o cateto adjacente. No caso da fórmula que calcula o “dx” e o “dy” que é a direção da arma do personagem, a hipotenusa (H) é o 20. No caso do seno de 30°, temos a seguinte resolução:
O resultado acima é somado com a coordenada y atual do personagem, assim obtemos o dy.
O deslocamento do personagem vai acontecer apenas com duas teclas: cima e baixo. As teclas esquerda e direita vão ser responsáveis pela rotação do personagem, o valor de rotação do personagem é que vai definir para onde o personagem irá se deslocar.
A função responsável pelo deslocamento e rotação do personagem será o “movePlayer”. Essa função será chamada dentro do “draw”.
function movePlayer() {
// Coordenadas de destino do personagem
let dx = 0, dy = 0;
// Avança para frente
if (keyIsDown(UP_ARROW)) {
dy = sin(player.angle) * (player.speed * deltaTime);
dx = cos(player.angle) * (player.speed * deltaTime);
}
// Recua para trás
if (keyIsDown(DOWN_ARROW)) {
dy = -sin(player.angle) * (player.speed * deltaTime);
dx = -cos(player.angle) * (player.speed * deltaTime);
}
// Roda o personagem para a esquerda
if (keyIsDown(LEFT_ARROW)) {
player.angle += 0.025 * (player.speed * deltaTime);
}
// Roda o personagem para a direita
if (keyIsDown(RIGHT_ARROW)) {
player.angle -= 0.025 * (player.speed * deltaTime)
}
// Calcula a coluna e linha dentro do mapa que o personagem se encontra
let currentColumn = floor((player.x + dx) / TILE_SIZE);
let currentRow = floor((player.y + dy) / TILE_SIZE);
// Só muda a coordenada atual do personagem se não for parede
if (MAP[currentRow][currentColumn] == 0) {
player.x += dx;
player.y += dy;
}
}
Dentro das condições “keyIsDown(UP_ARROW)” e keyIsDown(DOWN_ARROW)" temos cálculos trigonométricos. O seno positivo do ângulo atual do personagem retorna o eixo X, valor usado na coordenada X do personagem para representar a localidade horizontal. O seno negativo é a mesma coisa, só muda o sinal. O cosseno positivo do ângulo atual do personagem retorna o eixo Y, valor usado na coordenada Y do personagem para representar a localidade vertical.
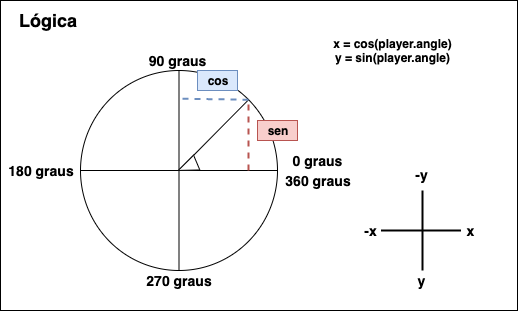
O gráfico acima mostra como funciona a lógica da rotação e do deslocamento do personagem. As setas direita e esquerda simplesmente giram o ângulo do personagem. Porém, quando o personagem se desloca, é necessário calcular o seno e o cosseno do ângulo atual. Como mostra no gráfico acima, o cosseno (linha azul na horizontal) representa a direção X que o personagem se deslocará. Enquanto o seno (linha vermelha na vertical) do ângulo do personagem representa a direção Y.
Na parte inferior na direita também mostra como os sinais funcionam no P5. Se o personagem se deslocar para cima, o Y será negativo e se for ao contrário (para baixo) o Y será positivo. A mesma regra vale para o X que é positivo pra direita e negativo pra esquerda.
Ao apertar a tecla “espaço”, rajadas vão ser disparadas exatamente de dentro da arma do personagem. O ângulo do tiro vai ser igual ao ângulo do personagem quando disparada a arma. Porém, o ângulo do tiro do personagem deve ser independente do ângulo de direção do personagem, e acima de tudo constante. Uma vez que o tiro encontra a parede, ele desaparece e é removido do jogo.
Primeiro, instanciamos a classe do tiro que será chamada de “bullet”. Os atributos dessa classe serão exatamente iguais ao da classe “Player”, com excessão do ângulo que será passado como parâmetro na instanciação do tiro.
class Bullet {
constructor(x, y, angle) {
this.x = x;
this.y = y;
this.scale = 10;
this.angle = angle;
this.speed = 1;
}
draw() {
let dy = this.y + sin(this.angle) * this.scale;
let dx = this.x + cos(this.angle) * this.scale;
line(this.x, this.y, dx, dy);
}
move() {
let dy = sin(this.angle) * (this.speed * deltaTime);
let dx = cos(this.angle) * (this.speed * deltaTime);
this.x += dx;
this.y += dy;
}
}
A função “draw” simplesmente exibirá os tiros na tela seguindo a mesma lógica do cálculo trigonométrico do personagem. Assim, podendo calcular a inclinação da bala baseando-se no ângulo em que a bala foi disparada. A função “move” calcula o deslocamento dos tiros.
Uma vez que a classe está pronta, podemos começar a implementar os tiros dentro da função “movePlayer”.
// Valor em milisegundos que o jogo está rodando
let milliNow = millis();
// Diferença entre o tempo em milisegundos entre o último tiro e agora
let milliDiff = milliNow - lastMilli;
// 32 representa a tecla espaço. Apenas 1 tiro a cada 200 milisegundos é permitido (0,2 segundos), isso é 5 tiros/s
if (keyIsDown(32) && (milliDiff > 200 || milliDiff < 0)) {
// Armazena o tempo que o último tiro foi dado
lastMilli = millis();
// Instancia os tiros
let bullet = new Bullet(player.x, player.y, player.angle);
bullets.push(bullet);
}
As variáveis “lastMilli” e “bullets” são variáveis de escopo global, podendo ser acessadas de qualquer local. “bullets” é um array contendo todos os tiros que aparecem na tela.
Em seguida, dentro da função “draw”, exibimos e deslocamos os tiros. Sem se esquecer das colisões dos tiros com a parede.
for (let i = 0; i < bullets.length; i++) {
// Seleciona um tiro por vez
let bullet = bullets[i];
// Exibi o tiro
bullet.draw();
// Desloca o tiro
bullet.move();
// Coluna atual que o tiro se encontra no mapa
let currentColumn = floor(bullet.x / TILE_SIZE);
// Linha atual que o tiro se encontra no mapa
let currentRow = floor(bullet.y / TILE_SIZE);
// Detecção de colisões
if (MAP[currentRow][currentColumn] == IS_WALL) {
bullets.splice(i, 1);
}
}
Finalmente podemos executar o projeto e visualizar os tiros.

A matemática é essencial para o desenvolvimento de jogos. Quanto mais complexo o jogo se torna, mais a matemática se torna importante, pois ela facilita o entendimento da lógica do jogo. As fórmulas de trigonometria podem ser lidas por qualquer pessoa familiarizada com o conceito matemático. Portanto, a matemática é indispensável para o desenvolvimento de jogos.
Geralmente, o ângulo da direção da arma do personagem é controlado pelo mouse do usuário, porém esse foi apenas um esqueleto de um jogo 2d visto de cima.
Postagens mais vistas

Os 5 principais componentes do computador são a unidade de controle, unidade aritmética e lógica, memória, dispositivo de entrada e dispositivo de saída.
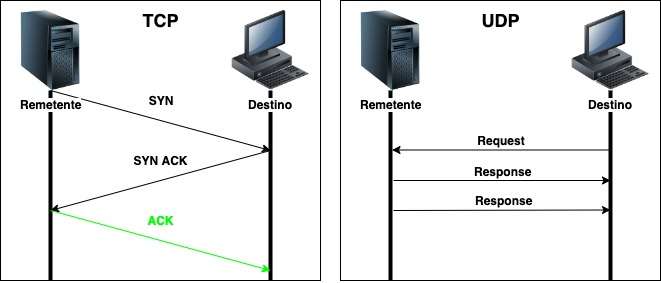
A porta é um número de 16 bits que é adicionado no final do endereço IP, insinuando qual aplicativo está vinculado e atuando nessa porta.
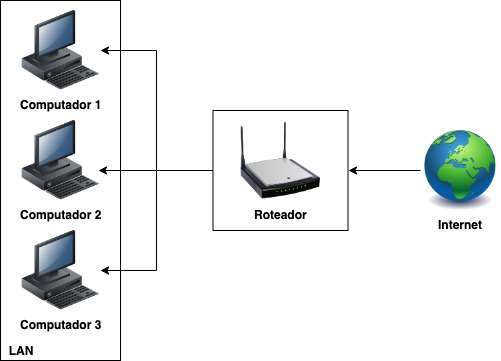
Rede local de computadores (LAN) é um conjunto de computadores ou dispositivos conectados uns aos outros de forma isolada em um pequeno local.